/Szkoła średnia/Równania/Wielomianowe/Stopnia 5/Różne

Zadanie nr 7991337

Uzasadnij, że wielomian 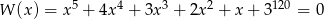5 4 3 2 120 W (x) = x + 4x + 3x + 2x + x+ 3 = 0 nie ma pierwiastków wymiernych.

Wersja PDF

Rozwiązanie

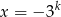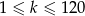Na mocy twierdzenia o wymiernych pierwiastkach wielomianu pierwiastek wymierny danego wielomianu musiałby mieć postać x = −3k dla 1 ≤ k ≤ 120 (pierwiastek nie może być dodatni, bo dla liczb dodatnich wartości wielomianu są dodatnie i łatwo sprawdzić, że nie może być równy 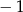− 1 , więc możemy założyć, że 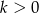k > 0 ). Sprawdźmy, czy liczba tej postaci może być pierwiastkiem wielomianu W (x) .

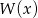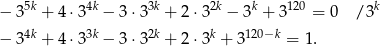
5k 4k 3k 2k k 120 k − 3 + 4 ⋅3 − 3⋅3 + 2 ⋅3 − 3 + 3 = 0 /3 − 3 4k + 4 ⋅33k − 3⋅3 2k + 2 ⋅3k + 3120−k = 1.

Jeżeli 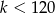k < 120 , to lewa strona dzieli się przez 3, a prawa nie, więc musi być 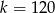k = 120 i mamy

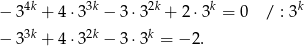
4k 3k 2k k k − 3 + 4 ⋅3 − 3⋅ 3 + 2 ⋅3 = 0 / : 3 − 33k + 4 ⋅32k − 3⋅ 3k = − 2.

Lewa strona znowu dzieli się przez 3, a prawa nie, więc liczba postaci 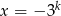k x = − 3 nie może być pierwiastkiem danego wielomianu.

Wersja PDF