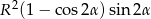/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Wpisany w okrąg

Zadanie nr 1454465

Dodaj do ulubionych
Dodaj do rozwiązanych

W kole o promieniu 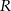R poprowadzono średnicę 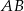AB i równoległą do niej cięciwę 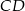CD . Oblicz pole powstałego trapezu 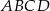ABCD , jeżeli kąt ostry tego trapezu ma miarę α .

Rozwiązanie

Zacznijmy od rysunku.

PIC

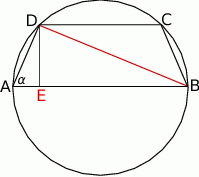
Ponieważ 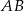AB jest średnicą okręgu więc trójkąt 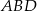ABD jest prostokątny. W szczególności

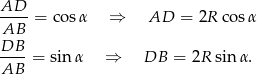
AD--= cosα ⇒ AD = 2R cosα AB DB ----= sin α ⇒ DB = 2R sin α. AB

Naszym celem jest wyliczenie długości podstaw i wysokości trapezu – aby to zrobić przyjrzyjmy się trójkątowi prostokątnemu 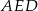AED .

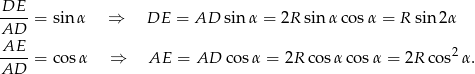
DE ----= sin α ⇒ DE = AD sin α = 2R sin αcos α = R sin 2α AD AE--= cosα ⇒ AE = AD co sα = 2R cosα cosα = 2R cos2 α. AD

Stąd mamy

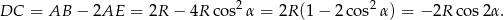
DC = AB − 2AE = 2R − 4R cos2α = 2R(1 − 2 cos2α ) = − 2R cos2 α.

Możemy więc policzyć szukane pole

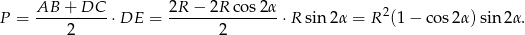
AB + DC 2R − 2R cos 2α P = ----------⋅DE = --------------- ⋅R sin 2α = R2(1 − cos 2α) sin 2α. 2 2

 
Odpowiedź: R 2(1− cos2 α)sin2 α

Wersja PDF