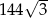Zadanie nr 4644578
W okrąg o średnicy 26 wpisano trapez równoramienny w ten sposób, że suma kwadratów długości jego podstaw jest równa 914, a sinus kąta ostrego wynosi 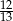 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
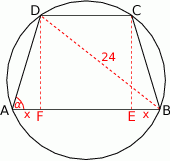
Zauważmy, że z podanego sinusa i średnicy okręgu możemy wyliczyć długość przekątnej 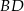 . Stosujemy twierdzenie sinusów w trójkącie
. Stosujemy twierdzenie sinusów w trójkącie 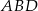 .
.
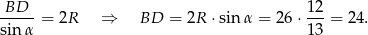
Chcielibyśmy teraz jakoś wykorzystać trójkąt prostokątny 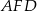 . Zanim to jednak zrobimy obliczmy
. Zanim to jednak zrobimy obliczmy 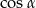 i
i 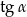 .
.
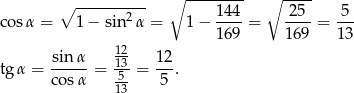
Jeżeli oznaczymy 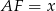 to mamy
to mamy
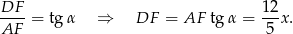
Teraz piszemy twierdzenie Pitagorasa w trójkącie 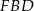 .
.
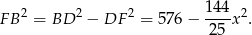
Teraz łatwo się zaciąć, bo nie bardzo widać jak sensownie wykorzystać podaną sumę kwadratów długości podstaw. Nie zrażajmy się jednak, że nie potrafimy ładnie wyliczyć  – okazuje się, że nie ma to większego znaczenia. Rzeczywiście,
– okazuje się, że nie ma to większego znaczenia. Rzeczywiście,
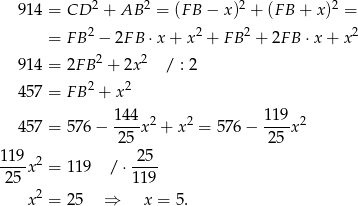
W takim razie
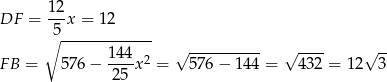
i pole trapezu jest równe
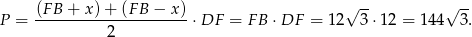
Odpowiedź: