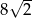Zadanie nr 7092986
Na trapezie równoramiennym o podstawach 2 i 6 opisano okrąg. Oblicz pole trapezu, jeśli dłuższa podstawa jest średnicą tego okręgu.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
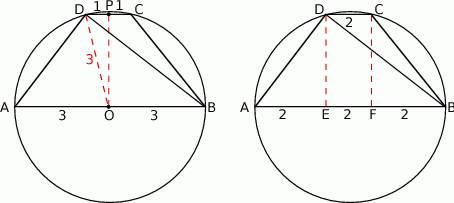
Sposób I
Jeżeli połączymy środek okręgu  (czyli też środek podstawy
(czyli też środek podstawy  ) z wierzchołkiem
) z wierzchołkiem 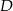 oraz ze środkiem
oraz ze środkiem 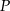 podstawy
podstawy 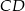 to otrzymamy trójkąt prostokątny
to otrzymamy trójkąt prostokątny 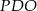 , w którym znamy długości odcinków:
, w którym znamy długości odcinków: 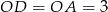 oraz
oraz 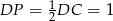 . Zatem
. Zatem
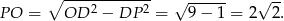
Obliczona długość odcinka 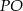 to dokładnie długość wysokości trapezu, zatem jego pole jest równe
to dokładnie długość wysokości trapezu, zatem jego pole jest równe
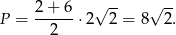
Sposób II
Ponieważ 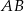 jest średnicą okręgu, trójkąt
jest średnicą okręgu, trójkąt 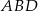 jest prostokątny. Znamy długość jego przeciwprostokątnej oraz wiemy na jakie odcinki dzieli ją wysokość opuszczona z wierzchołka
jest prostokątny. Znamy długość jego przeciwprostokątnej oraz wiemy na jakie odcinki dzieli ją wysokość opuszczona z wierzchołka 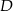 – to powinno pozwolić nam wyliczyć jego wysokość.
– to powinno pozwolić nam wyliczyć jego wysokość.
Zauważmy, że trójkąty 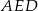 i
i 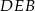 są podobne (bo oba są podobne do trójkąta
są podobne (bo oba są podobne do trójkąta 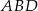 ). Zatem
). Zatem
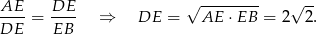
Zatem pole trapezu jest równe
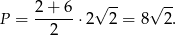
Odpowiedź: