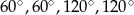Zadanie nr 8131206
Punkt 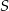 jest środkiem okręgu opisanego na trapezie równoramiennym
jest środkiem okręgu opisanego na trapezie równoramiennym 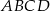 . Kąt
. Kąt 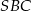 jest dwa razy większy od kąta
jest dwa razy większy od kąta 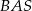 , a kąt
, a kąt 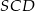 jest dwa razy większy od kąta
jest dwa razy większy od kąta 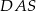 . Oblicz kąty trapezu
. Oblicz kąty trapezu 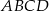 .
.
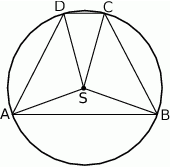
Rozwiązanie
Oznaczmy 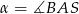 .
.
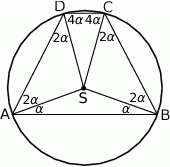
Trójkąty 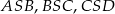 i
i 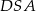 są równoramienne oraz
są równoramienne oraz 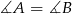 , więc z podanych informacji mamy
, więc z podanych informacji mamy
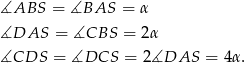
Suma kątów trapezu 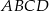 jest równa
jest równa 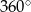 , więc
, więc
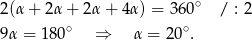
W takim razie kąty trapezu 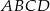 mają miary
mają miary
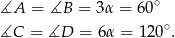
Odpowiedź: