Zadanie nr 9779225
Trapez równoramienny 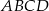 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 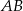 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 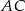 i
i 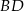 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 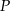 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 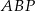 .
.
Rozwiązanie
Narysujmy opisaną sytuację.
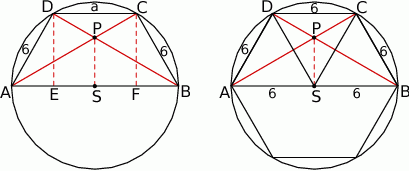
Ponieważ podstawa 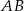 jest średnicą okręgu, trójkąt
jest średnicą okręgu, trójkąt 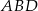 jest prostokątny, skąd
jest prostokątny, skąd
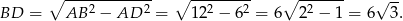
Obliczmy teraz wysokość 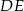 trójkąta
trójkąta 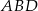 (a więc również wysokość trapezu). Porównujemy dwa wzory na pole (inny sposób to wykorzystać podobieństwo trójkątów
(a więc również wysokość trapezu). Porównujemy dwa wzory na pole (inny sposób to wykorzystać podobieństwo trójkątów 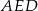 i
i 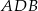 ).
).
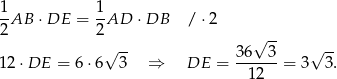
Obliczamy teraz długość 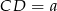 drugiej postawy trapezu. Z trójkąta prostokątnego
drugiej postawy trapezu. Z trójkąta prostokątnego 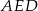 mamy
mamy
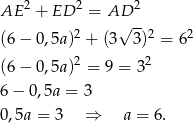
Zauważmy teraz, że trójkąty 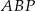 i
i 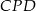 są podobne (bo mają równe kąty) oraz znamy skalę ich podobieństwa:
są podobne (bo mają równe kąty) oraz znamy skalę ich podobieństwa: 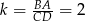 . W takim razie
. W takim razie
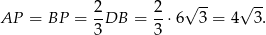
Łatwo też obliczyć pole trójkąta 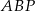 .
.
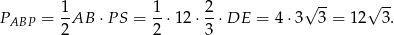
Promień  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 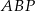 obliczamy korzystając ze wzoru na pole
obliczamy korzystając ze wzoru na pole
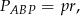
gdzie
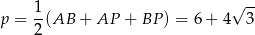
jest połową obwodu trójkąta 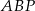 . Mamy zatem
. Mamy zatem
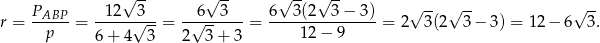
Pole koła jest więc równe
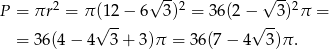
Sposób II
Zanim zabierzemy się za rachunki przyjrzyjmy się dokładniej sytuacji opisanej w treści zadania. Zauważmy, że każdy z trójkątów 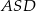 i
i 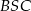 jest równoramienny:
jest równoramienny:
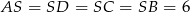
To w połączeniu z długością ramienia trapezu równą 6 oznacza, że każdy z tych dwóch trójkątów jest równoboczny. W takim razie równoboczny jest też trójkąt 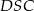 (bo
(bo 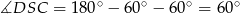 oraz
oraz 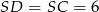 ). To oznacza, że dany trapez to połowa sześciokąta foremnego wpisanego w okrąg. Jeżeli oznaczamy przez
). To oznacza, że dany trapez to połowa sześciokąta foremnego wpisanego w okrąg. Jeżeli oznaczamy przez
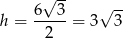
długość wysokości w trójkącie równobocznym boku długości 6, to mamy
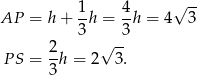
W takim razie pole i połowa obwodu trójkąta 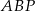 są równe
są równe
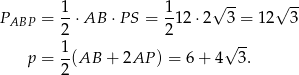
Promień i pole koła wpisanego w trójkąt 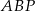 obliczamy tak samo jak w pierwszym sposobie.
obliczamy tak samo jak w pierwszym sposobie.
Odpowiedź: