/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Pole

Zadanie nr 7342590

Odcinek 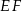EF łączący środki dwóch dłuższych boków prostokąta 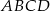ABCD dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta ABCD .

PIC

Wersja PDF

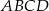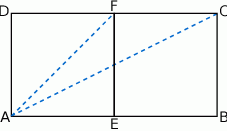
Rozwiązanie

Jeżeli oznaczymy przez a długość boku każdego z kwadratów, to mamy

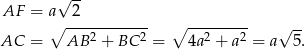
√ -- AF = a∘ -2---------- ∘ --------- √ -- AC = AB 2 + BC 2 = 4a2 + a2 = a 5.

Mamy zatem równanie

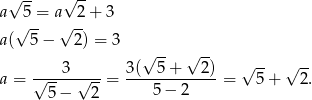
√ -- √ -- a √5-= a√ 2-+ 3 a( 5− 2) = 3 √ -- √ -- √---3-√--- 3(--5-+---2)- √ -- √ -- a = 5 − 2 = 5− 2 = 5+ 2.

Pole prostokąta jest więc równe

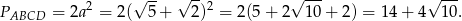
√ -- √ -- √ --- √ --- P = 2a2 = 2 ( 5+ 2)2 = 2(5 + 2 10 + 2) = 1 4+ 4 10. ABCD

 
Odpowiedź: √ --- 14 + 4 1 0

Wersja PDF