/Szkoła średnia/Geometria/Geometria analityczna/Odcinek

Zadanie nr 8364191

Dodaj do ulubionych
Dodaj do rozwiązanych

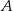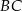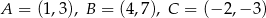Oblicz odległość punktu A od środka odcinka BC , gdzie A = (1,3), B = (4,7), C = (− 2,− 3) .

Rozwiązanie

Żeby wiedzieć o co chodzi, możemy zacząć od szkicowego rysunku.

PIC

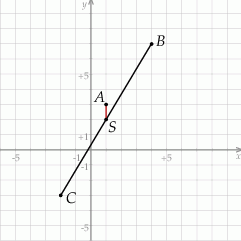
Środek 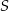S odcinka 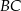BC ma współrzędne

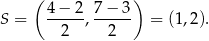
( ) S = 4-−-2, 7-−-3 = (1,2). 2 2

Zatem długość odcinka 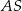AS jest równa

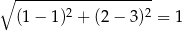
∘ ------------------- (1− 1)2 + (2 − 3)2 = 1

(mogliśmy też od razu zauważyć, że oba punkty leżą na wspólnej pionowej prostej, więc ich odległość to po prostu różnica drugich współrzędnych).  
Odpowiedź: 1

Wersja PDF