Zadanie nr 9287114
Wyznacz współrzędne punktu 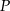 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 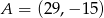 i
i 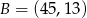 w stosunku
w stosunku 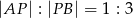 .
.
Rozwiązanie
Sposób I
Jeżeli zrobimy obrazek, to łatwo zauważyć, że aby otrzymać punkt 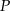 musimy podzielić odcinek
musimy podzielić odcinek 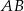 na 4 części i punkt
na 4 części i punkt 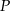 to koniec pierwszego odcinka.
to koniec pierwszego odcinka.
Innymi słowy, musimy wyznaczyć środek 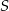 odcinka
odcinka 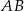 , a punkt
, a punkt 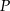 jest środkiem odcinka
jest środkiem odcinka 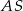 . Liczymy
. Liczymy
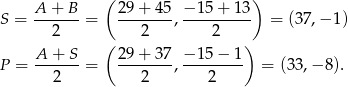
Sposób II
Zadanie łatwo też rozwiązać używając wektorów. Szukany punkt 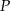 otrzymamy przesuwając punkt
otrzymamy przesuwając punkt 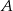 o
o 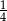 wektora
wektora 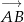 . Zatem
. Zatem
![P = A + 1-−A→B = (29 ,− 1 5)+ 1[16,28] = (29,− 15 )+ [4,7] = (33 ,− 8 ). 4 4](https://img.zadania.info/zad/9287114/HzadR13x.gif)
Sposób III
Punkt 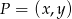 możemy wyznaczyć z równości:
możemy wyznaczyć z równości: 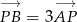 . Liczymy
. Liczymy
![[{45− x,13 − y] = 3[x − 29,y + 15] 45 − x = 3x− 87 13 − y = 3y+ 45 { 132 = 4x ⇒ x = 33 − 32 = 4y ⇒ y = − 8.](https://img.zadania.info/zad/9287114/HzadR16x.gif)
Odpowiedź: