/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Liceum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 28 marca 2015 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 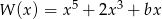 jest podzielny przez wielomian
jest podzielny przez wielomian 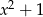 . Wynika stąd, że
. Wynika stąd, że
A) 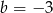 B)
B) 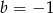 C)
C) 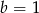 D)
D) 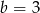
Liczba 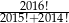 jest równa
jest równa
A) 2015 B) 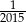 C) 1 D) 2016
C) 1 D) 2016
Która z poniższych funkcji nie ma ekstremów lokalnych?
A) 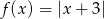 B)
B) 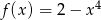 C)
C) 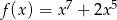 D)
D) 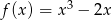
Okrąg 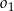 ma równanie
ma równanie 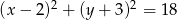 , a okrąg
, a okrąg 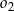 ma równanie
ma równanie 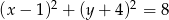 . Określ wzajemne położenie tych okręgów.
. Określ wzajemne położenie tych okręgów.
A) Te okręgi przecinają się w dwóch punktach.
B) Te okręgi są styczne.
C) Te okręgi nie mają punktów wspólnych oraz okrąg 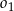 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 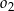 .
.
D) Te okręgi nie mają punktów wspólnych oraz okrąg 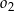 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 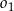 .
.
W pokoju w kilkunastu ponumerowanych workach znajdują się kolorowe piłki. Miłosz z zamkniętymi oczami wybiera losowo jeden z tych worków, a potem z wybranego worka wybiera jedną piłkę. Prawdopodobieństwo wybrania białej piłki z worka numer 1 jest równe 0,3, a prawdopodobieństwo, że Miłosz wybierze worek numer 1 jest równe 0,4. Jakie jest prawdopodobieństwo tego, że Miłosz wybierze worek numer 1 i z tego worka wyjmie piłkę, która nie jest biała?
A) 0,7 B) 0,9 C) 0,12 D) 0,28
Zadania otwarte
Rozwiąż równanie 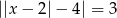 .
.
Oblicz granicę 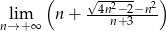 .
.
Funkcja 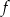 jest określona wzorem
jest określona wzorem 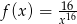 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 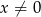 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 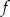 w punkcie
w punkcie 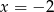 .
.
Oblicz 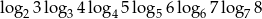 .
.
Oblicz pole trójkąta ograniczonego przez osie układu współrzędnych oraz styczną do wykresu funkcji 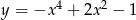 w punkcie
w punkcie 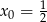 .
.
Rozwiąż równanie 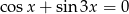 .
.
Wykaż, że
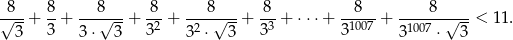
Na bokach 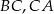 i
i 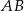 trójkąta
trójkąta 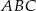 wybrano punkty
wybrano punkty 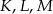 takie, że
takie, że
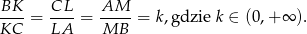
Oblicz stosunek pola trójkąta 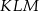 do pola trójkąta
do pola trójkąta 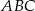 .
.
Wyznacz największą wartość funkcji 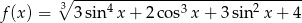 .
.
Przekątna 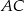 równoległoboku
równoległoboku 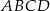 tworzy z jego bokami kąty o miarach
tworzy z jego bokami kąty o miarach 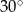 i
i 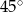 . Oblicz stosunek
. Oblicz stosunek 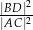 kwadratów długości przekątnych tego równoległoboku.
kwadratów długości przekątnych tego równoległoboku.
W pierwszej urnie są kule czarne i białe, w drugiej 10 kul niebieskich i 15 kul zielonych, a w trzeciej – 14 kul niebieskich i 7 zielonych. Najpierw losujemy kulę z pierwszej urny, a następnie losujemy kulę z drugiej albo z trzeciej urny w zależności od tego, czy z pierwszej urny wylosowaliśmy odpowiednio kulę białą, czy czarną. Oblicz prawdopodobieństwo wylosowania czarnej kuli z pierwszej urny, jeżeli prawdopodobieństwo wylosowania według opisanego schematu kuli niebieskiej jest takie samo jak zielonej.
Podstawą ostrosłupa 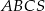 jest trójkąt równoramienny
jest trójkąt równoramienny 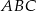 , w którym
, w którym 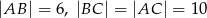 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt
, a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 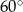 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wyznacz wszystkie proste, które są jednocześnie styczne do paraboli 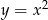 oraz okręgu o równaniu
oraz okręgu o równaniu 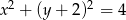 .
.

