/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Liceum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 18 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Dla każdej liczby  , spełniającej warunek
, spełniającej warunek 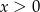 , wyrażenie
, wyrażenie 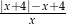 jest równe
jest równe
A) 2 B) 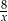 C)
C) 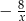 D) 4
D) 4
Punkty 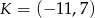 i
i 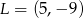 to środki boków, odpowiednio
to środki boków, odpowiednio 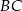 i
i 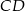 kwadratu
kwadratu 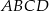 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 32 B) 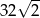 C)
C) 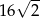 D) 16
D) 16
Po dwukrotnej obniżce ceny, za każdym razem o 5%, kurtka kosztowała 245,48 zł. Jej cena początkowa to:
A) 270,64 zł B) 270 zł C) 272 zł D) 250 zł
Liczba 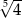 jest większa od
jest większa od
A) 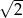 B)
B) 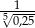 C)
C) 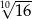 D)
D) 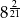
Liczba 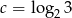 . Wtedy
. Wtedy
A) 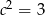 B)
B) 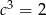 C)
C) 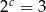 D)
D) 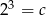
Wyrażenie 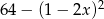 jest równe
jest równe
A) 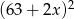 B)
B) 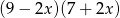 C)
C) 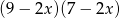 D)
D) 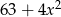
Liczba 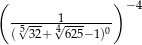 jest równa
jest równa
A) 1 B)  C) 6 D) 1296
C) 6 D) 1296
Rozwiązaniem nierówności 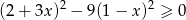 jest zbiór
jest zbiór
A) 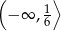 B)
B) 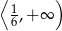 C)
C) 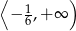 D)
D) 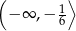
Układ równań 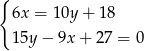
A) ma dokładnie jedno rozwiązanie.
B) ma dwa rozwiązania.
C) ma nieskończenie wiele rozwiązań.
D) nie ma rozwiązań.
Punkt 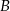 jest symetryczny do punktu
jest symetryczny do punktu 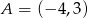 względem osi
względem osi 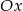 układu współrzędnych, a punkt
układu współrzędnych, a punkt 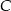 jest symetryczny do punktu
jest symetryczny do punktu 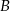 względem osi
względem osi 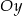 . Zatem trójkąt
. Zatem trójkąt 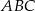 jest
jest
A) równoboczny
B) prostokątny i równoramienny
C) prostokątny i żaden z jego kątów nie jest równy 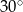
D) prostokątny z kątem ostrym równym 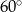
Funkcja 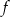 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 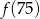 ,
, 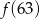 ,
, 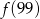 ,
, 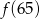 największa to
największa to
A) 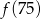 B)
B) 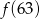 C)
C) 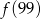 D)
D) 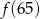
Z prostopadłościanu 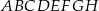 odcięto ostrosłup
odcięto ostrosłup 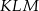 w ten sposób, że punkty
w ten sposób, że punkty 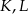 i
i 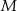 są środkami krawędzi
są środkami krawędzi 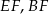 i
i  (zobacz rysunek).
(zobacz rysunek).
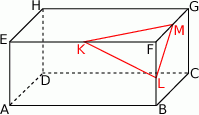
Ile razy objętość odciętego ostrosłupa jest mniejsza od objętości pozostałej części prostopadłościanu?
A) 48 razy. B) 47 razy. C) 46 razy. D) 24 razy.
Osią symetrii paraboli będącej wykresem funkcji 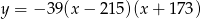 jest prosta o równaniu
jest prosta o równaniu
A) 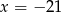 B)
B) 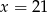 C)
C) 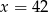 D)
D) 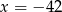
Ciąg geometryczny 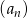 określony jest wzorem
określony jest wzorem 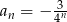 dla
dla 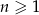 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 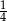 B)
B) 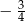 C)
C)  D)
D) 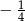
Wspólnym pierwiastkiem równań 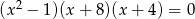 oraz
oraz 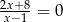 jest liczba
jest liczba
A) 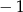 B) 1 C)
B) 1 C) 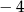 D)
D) 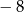
Dane są równania czterech prostych:
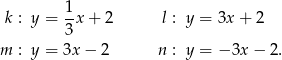
Prostopadłe są proste
A) 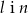 B)
B) 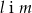 C)
C) 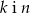 D)
D) 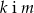
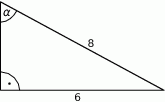
W trójkącie, przedstawionym na rysunku poniżej, cosinus kąta ostrego  jest równy
jest równy
A)  B)
B)  C)
C) 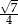 D)
D) 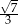
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 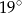 i
i 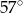 .
.
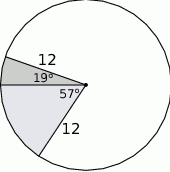
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 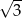
Dane są dwa okręgi o promieniach 8 i 13. Okręgi te są styczne wewnętrznie, gdy odległość ich środków jest równa
A) 8 B) 21 C) 5 D) 13
Ze zbioru 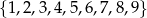 wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
A) 72 B) 36 C) 81 D) 17
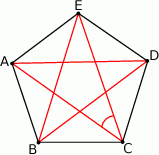
Punkty 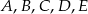 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta 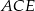 jest równa
jest równa
A) 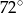 B)
B) 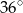 C)
C) 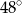 D)
D) 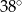
Ciąg 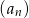 określony jest wzorem
określony jest wzorem 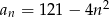 , gdzie
, gdzie 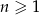 . Liczba nieujemnych wyrazów tego ciągu jest równa
. Liczba nieujemnych wyrazów tego ciągu jest równa
A) 11 B) 22 C) 10 D) 5
Rzucamy 10 razy symetryczną monetą. Niech 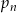 dla
dla 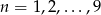 oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach
oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach  i
i 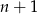 . Wtedy
. Wtedy
A) 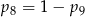 B)
B) 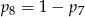 C)
C) 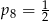 D)
D) 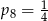
Które z podanych równań nie ma rozwiązań
A) 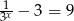 B)
B) 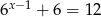 C)
C) 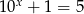 D)
D) 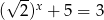
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Zadania otwarte
Rozwiązaniem nierówności 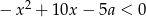 jest zbiór
jest zbiór 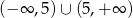 . Wyznacz
. Wyznacz  .
.
Uzasadnij, że żadna liczba rzeczywista nie jest rozwiązaniem równania 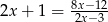 .
.
W ciągu arytmetycznym 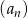 dane są wyrazy:
dane są wyrazy: 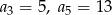 . Oblicz, ile wyrazów ciągu
. Oblicz, ile wyrazów ciągu 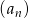 jest mniejszych niż 83.
jest mniejszych niż 83.
Wykaż, że jeżeli pole koła opisanego na trójkącie prostokątnym jest 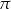 razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
Punkty 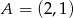 i
i 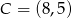 są przeciwległymi wierzchołkami prostokąta, którego bok
są przeciwległymi wierzchołkami prostokąta, którego bok 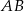 jest równoległy do osi
jest równoległy do osi 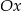 . Punkty
. Punkty 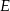 i
i 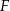 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 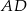 i
i 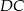 . Oblicz pole trójkąta
. Oblicz pole trójkąta 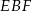 .
.
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba całkowita dodatnia mniejsza od 10000 jest czterocyfrowa.
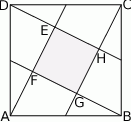
Wierzchołki kwadratu 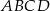 połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat
połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 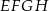 . Oblicz, jaki jest stosunek obwodów kwadratów
. Oblicz, jaki jest stosunek obwodów kwadratów 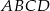 i
i 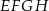 .
.
Punkty 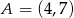 ,
, 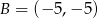 i
i 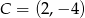 są wierzchołkami trapezu prostokątnego
są wierzchołkami trapezu prostokątnego 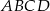 o podstawach
o podstawach 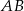 i
i 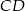 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 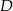 .
.
Tworząca stożka ma długość 25, a średnica podstawy stożka jest krótsza od wysokości stożka o 10. Oblicz pole powierzchni całkowitej i objętość tego stożka.

