/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Liceum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 7 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 22 jest przybliżeniem z nadmiarem liczby  . Błąd bezwzględny tego przybliżenia jest równy 0,34. Liczba
. Błąd bezwzględny tego przybliżenia jest równy 0,34. Liczba  to
to
A) 21,66 B) 21,70 C) 22,30 D) 22,34
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
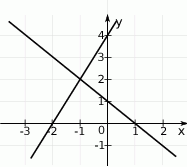
Wskaż ten układ
A) 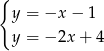 B)
B) 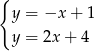 C)
C) 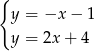 D)
D) 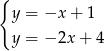
Cenę pewnego towaru obniżono o 20%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 25% D) o 30%
Liczbą odwrotną do 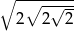 jest
jest
A) 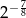 B)
B) 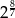 C)
C) 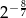 D)
D) 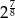
Suma 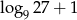 jest równa
jest równa
A) 3 B) 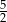 C)
C) 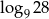 D)
D) 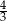
Wykres funkcji 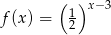 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
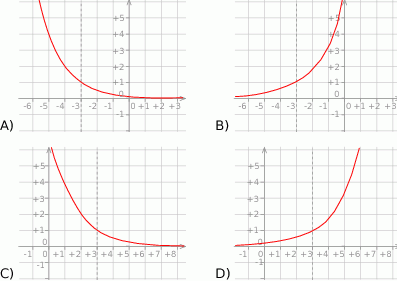
Wyrażenie 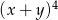 jest równe
jest równe
A) 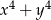
B) 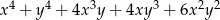
C) 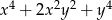
D) 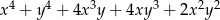
Przedział 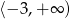 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 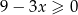 B)
B) 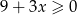 C)
C) 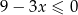 D)
D) 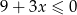
Na płaszczyźnie dane są punkty: 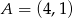 ,
, 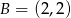 i
i 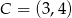 . Kąt
. Kąt 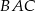 jest równy
jest równy
A) 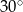 B)
B) 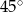 C)
C) 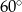 D)
D) 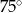
Liczba 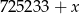 daje resztę 2 z dzielenia przez 9. Liczba
daje resztę 2 z dzielenia przez 9. Liczba  może być równa
może być równa
A) 2 B) 3 C) 7 D) 8
Zbiorem wartości funkcji 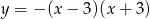 określonej dla
określonej dla 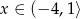 jest przedział
jest przedział
A) 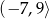 B)
B) 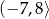 C)
C) 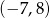 D)
D) 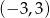
Objętość kuli wpisanej w sześcian o krawędzi długości 4 jest równa
A) 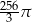 B)
B) 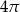 C)
C) 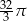 D)
D) 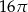
Wykresem funkcji kwadratowej 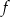 jest parabola o wierzchołku
jest parabola o wierzchołku 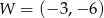 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 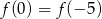 B)
B) 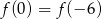 C)
C) 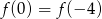 D)
D) 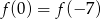
Punkt 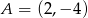 jest wierzchołkiem prostokąta
jest wierzchołkiem prostokąta 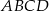 . Prosta o równaniu
. Prosta o równaniu 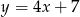 zawiera bok
zawiera bok 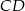 . Bok
. Bok 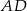 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 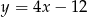 B)
B) 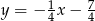 C)
C) 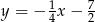 D)
D) 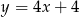
Równanie 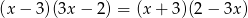 ma dwa rozwiązania. Są to liczby
ma dwa rozwiązania. Są to liczby
A) 0 oraz  B)
B) 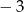 oraz
oraz  C)
C)  oraz 3 D)
oraz 3 D) 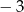 oraz 3
oraz 3
Pani Jolanta spłaciła kredyt w wysokości 20 000 zł w pięciu ratach, z których każda kolejna była o 600 zł mniejsza od poprzedniej. Pierwsza rata była równa:
A) 5 800 zł B) 4 800 zł C) 5 600 zł D) 5 200 zł
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 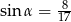 . Bok
. Bok 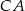 tego trójkąta ma długość:
tego trójkąta ma długość:
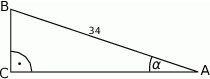
A) 30 B) 8 C) 16 D) 24
Liczby 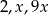 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 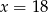 B)
B) 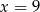 C)
C) 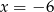 D)
D) 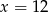
Dane są dwa okręgi o promieniach 10 i 18. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 18 B) 8 C) 10 D) 28
Wiadomo, że mediana liczb 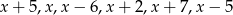 jest dwa razy większa od średniej tych liczb. Zatem liczba
jest dwa razy większa od średniej tych liczb. Zatem liczba 
A) jest równa 0 B) jest równa 1 C) jest równa 2 D) może mieć dowolną wartość
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 6, jest równe
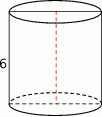
A) 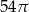 B)
B) 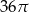 C)
C) 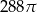 D)
D) 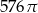
Ciąg 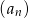 określony jest wzorem
określony jest wzorem 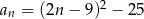 , gdzie
, gdzie 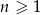 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 4 B) 5 C) 6 D) 7
Dla pewnego zdarzenia losowego 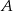 prawdziwe jest równanie (
prawdziwe jest równanie (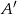 – zdarzenie przeciwne do zdarzenia
– zdarzenie przeciwne do zdarzenia 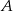 )
) 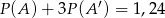 , zatem
, zatem
A) 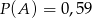 B)
B) 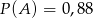 C)
C) 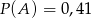 D)
D) 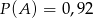
Zadania otwarte
Prosta 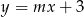 tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz
tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz  .
.
Udowodnij, że jeżeli 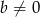 i
i 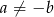 , to
, to 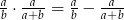 .
.
Niech 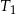 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 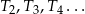 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów 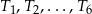 .
.
Rozwiąż równanie 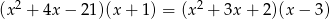 .
.
Okręgi 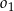 i
i 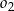 są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu
są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu 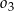 . Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa
. Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa 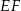 okręgu
okręgu 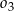 jest wspólną styczną okręgów
jest wspólną styczną okręgów 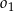 i
i 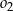 . Oblicz długość odcinka
. Oblicz długość odcinka 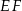 jeżeli promienie okręgów
jeżeli promienie okręgów 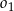 i
i 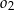 są odpowiednio równe
są odpowiednio równe 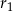 i
i 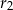 .
.
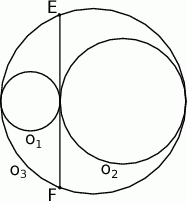
Punkty 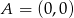 ,
, 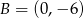 i
i 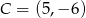 są wierzchołkami trapezu prostokątnego o polu 36 i podstawach
są wierzchołkami trapezu prostokątnego o polu 36 i podstawach 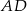 i
i 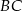 . Oblicz pole trójkąta
. Oblicz pole trójkąta 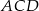 .
.
Uzasadnij, że suma kwadratów trzech kolejnych liczb parzystych nigdy nie jest liczbą podzielną przez 3.
Grupę uczniów ustawiono w dwuszeregu: w pierwszym szeregu ustawiono 8 osób, a w drugim 10. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że dwie losowo wybrane osoby stoją w tym samym szeregu i obok siebie?
Punkt 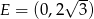 jest środkiem boku
jest środkiem boku 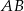 trójkąta równobocznego
trójkąta równobocznego 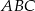 , prosta
, prosta 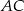 ma równanie
ma równanie 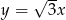 , a początek układu współrzędnych pokrywa się wierzchołkiem
, a początek układu współrzędnych pokrywa się wierzchołkiem 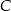 tego trójkąta. Napisz równania wysokości trójkąta
tego trójkąta. Napisz równania wysokości trójkąta 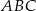 przechodzących przez wierzchołki
przechodzących przez wierzchołki 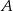 i
i 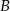 .
.
Podstawą ostrosłupa prawidłowego jest trójkąt równoboczny. Wysokość ściany bocznej tego ostrosłupa jest równa 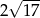 , a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.
, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 4. Oblicz objętość tego ostrosłupa.