/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Liceum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 21 marca 2015 Czas pracy: 180 minut
Zadania zamknięte
Dla której z podanych funkcji granica prawostronna 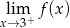 jest skończona?
jest skończona?
A) 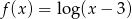 B)
B) 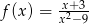 C)
C) 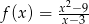 D)
D) 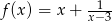
Układ równań 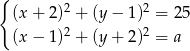 z niewiadomymi
z niewiadomymi 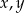 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 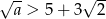 B)
B) 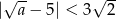 C)
C) 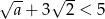 D)
D) 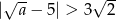
Niech 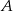 i
i 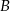 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 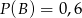 i
i 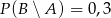 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 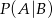 jest równe
jest równe
A) 0,3 B) 0,9 C) 0,5 D) 0,18
Każda liczba  należąca do przedziału otwartego
należąca do przedziału otwartego 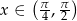 spełnia nierówność
spełnia nierówność
A) 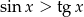 B)
B) 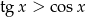 C)
C) 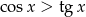 D)
D) 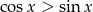
Ile miejsc zerowych ma funkcja 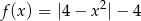 ?
?
A) 1 B) 2 C) 3 D) 4
Zadania otwarte
Oblicz 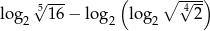 .
.
Oblicz granicę ciągu 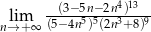 .
.
Dane są liczby 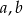 takie, że
takie, że 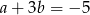 i
i 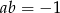 . Oblicz
. Oblicz 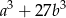 .
.
Wyznacz równanie okręgu o środku 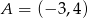 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 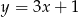 .
.
Reszta z dzielenia wielomianu 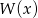 przez wielomian
przez wielomian 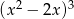 jest równa
jest równa 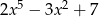 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 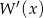 przez dwumian
przez dwumian 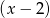 .
.
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 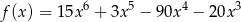 ma ekstrema lokalne.
ma ekstrema lokalne.
Dla jakich wartości parametru 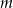 prosta
prosta 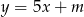 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 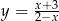 ?
?
Zbiór 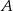 ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór
ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór 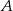 ?
?
Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie
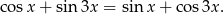
Dany jest nieskończony ciąg geometryczny 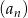 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 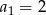 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 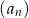 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Czworokąt 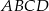 jest trapezem o podstawach
jest trapezem o podstawach 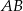 i
i 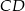 . Wykaż że
. Wykaż że
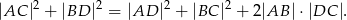
Suma długości wszystkich krawędzi prostopadłościanu jest równa 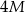 , a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.

