/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Technikum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 25 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 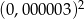 jest równa
jest równa
A) 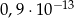 B)
B) 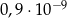 C)
C) 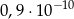 D)
D) 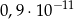
Suma liczby  i
i 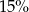 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 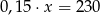 B)
B) 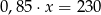 C)
C) 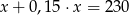 D)
D) 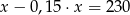
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 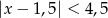 B)
B) 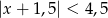 C)
C) 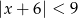 D)
D) 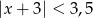
Iloczyn 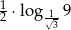 jest równy
jest równy
A) 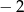 B)
B) 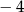 C)
C) 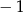 D) 1
D) 1
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 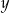 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 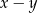 B)
B) 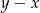 C)
C) 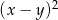 D)
D) 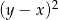
Rozwiązaniem równania 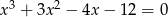 nie jest liczba
nie jest liczba
A) 2 B) 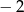 C)
C) 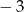 D) 3
D) 3
Liczba 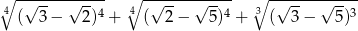 jest równa
jest równa
A) 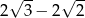 B)
B) 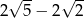 C)
C) 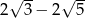 D)
D) 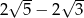
Wykres funkcji liniowej 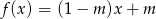 przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
przechodzi przez I, III i IV ćwiartkę układu współrzędnych wtedy i tylko wtedy, gdy
A) 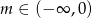 B)
B) 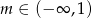 C)
C) 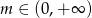 D)
D) 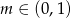
Wierzchołek paraboli 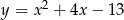 leży na prostej o równaniu
leży na prostej o równaniu
A) 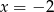 B)
B) 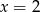 C)
C) 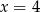 D)
D) 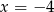
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 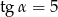 . Zatem
. Zatem
A) 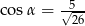 B)
B) 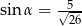 C)
C) 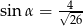 D)
D) 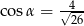
Nierówność 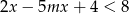 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 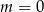 B)
B) 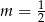 C)
C) 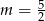 D)
D) 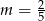
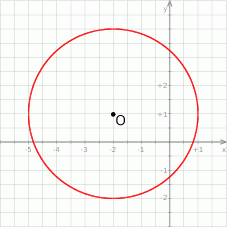
Punkt 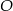 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
A) 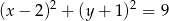
B) 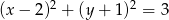
C) 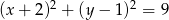
D) 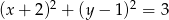
Do wykresu funkcji 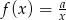 , dla
, dla 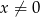 należy punkt
należy punkt 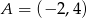 . Wtedy
. Wtedy
A) 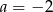 B)
B) 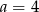 C)
C) 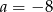 D)
D) 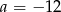
Odcinki 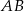 i
i 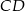 są równoległe i
są równoległe i 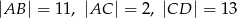 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 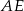 jest równa
jest równa
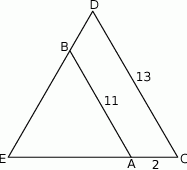
A) 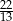 B)
B) 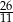 C) 11 D) 13
C) 11 D) 13
Wyraz wolny wielomianu 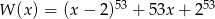 jest równy
jest równy
A) 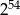 B) 0 C)
B) 0 C) 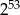 D) 53
D) 53
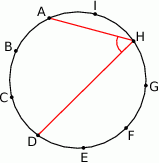
Punkty 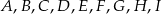 dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 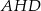 jest równa
jest równa
A) 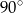 B)
B) 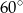 C)
C) 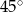 D)
D) 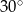
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 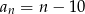 wynosi
wynosi
A) 8 B) 9 C) 10 D) 11
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 67035 B) 49629 C) 17022 D) 16919
Odcinki 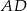 i
i 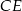 są wysokościami trójkąta
są wysokościami trójkąta 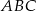 .
.
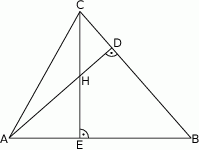
Zatem
A) 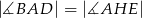
B) 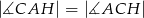
C) 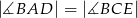
D) 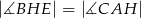
Na rysunku przedstawiono wykres funkcji 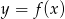 .
.
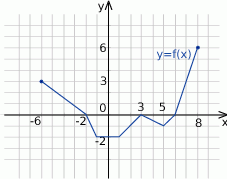
Zbiorem wartości funkcji 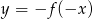 jest
jest
A) 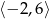 B)
B) 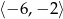 C)
C) 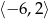 D)
D) 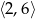
Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 90 B) 81 C) 82 D) 80
Kula ma objętość 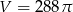 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
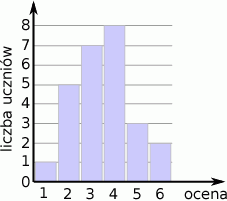
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
A) 2 B) 3 C) 3,5 D) 4
Zadania otwarte
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 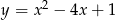 w przedziale
w przedziale 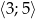 .
.
Iloczyn drugiego i czwartego wyrazu ciągu geometrycznego o wyrazach dodatnich jest równy 9. Oblicz iloczyn pięciu początkowych kolejnych wyrazów tego ciągu.
Oblicz wartość wyrażenia 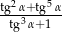 jeżeli
jeżeli 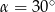 .
.
Uzasadnij, że jeśli 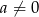 oraz
oraz 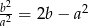 , to
, to 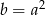 .
.
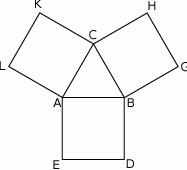
Na bokach trójkąta równobocznego 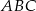 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 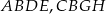 i
i 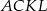 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 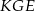 jest równoboczny.
jest równoboczny.
Wiadomo, że funkcja liniowa 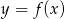 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 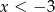 . Ponadto,
. Ponadto, 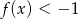 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 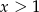 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 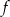 .
.
W pewnej szkole 47% uczniów uczęszcza na kółko plastyczne, a 65% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 30% uczniów uczęszcza na obydwa kółka. Oblicz prawdopodobieństwo, że losowy wybrany uczeń tej szkoły nie uczęszcza na żadne z tych kółek.
Wierzchołki trapezu 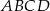 mają współrzędne:
mają współrzędne: 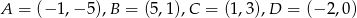 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 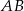 tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona
tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona 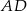 oraz
oraz 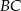 trapezu
trapezu 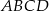 .
.
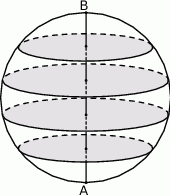
Drewnianą kulę o promieniu 5 cm pocięto na 5 części w ten sposób, że płaszczyzny cięcia są prostopadłe do ustalonej średnicy 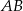 tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.
tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.