/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info/Technikum
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 14 marca 2015 Czas pracy: 180 minut
Rozwiąż nierówność 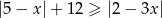 .
.
Wewnątrz prostokąta 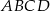 o wymiarach
o wymiarach 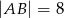 i
i 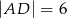 wybrano dwa punkty
wybrano dwa punkty 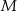 i
i 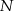 takie, że
takie, że 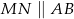 oraz
oraz 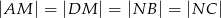 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 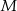 i
i 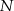 suma kwadratów długości odcinków
suma kwadratów długości odcinków 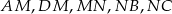 jest najmniejsza?
jest najmniejsza?
Wyznacz wszystkie wartości parametru 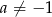 , dla których wykres funkcji
, dla których wykres funkcji 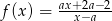 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 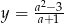 .
.
Rozwiąż równanie 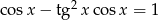 w przedziale
w przedziale 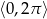 .
.
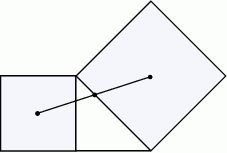
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
Ciąg 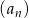 , gdzie
, gdzie 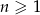 dany jest wzorem rekurencyjnym
dany jest wzorem rekurencyjnym
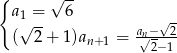
- Oblicz sumę 21 początkowych wyrazów tego ciągu.
- Wyznacz wszystkie liczby naturalne
 , dla których spełniona jest nierówność
, dla których spełniona jest nierówność 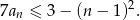
Udowodnij, że 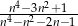 , dla
, dla 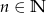 i
i 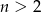 jest ułamkiem właściwym.
jest ułamkiem właściwym.
W trójkąt prostokątny 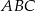 o przyprostokątnych długości
o przyprostokątnych długości 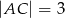 i
i 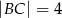 wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków
wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków 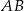 i
i  , a drugi do boków
, a drugi do boków 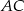 i
i 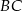 .
.
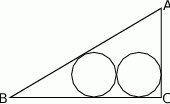
Oblicz długość promienia tych okręgów.
Reszta z dzielenia wielomianu 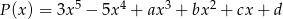 przez wielomian
przez wielomian 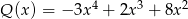 jest taka sama jak reszta z dzielenia wielomianu
jest taka sama jak reszta z dzielenia wielomianu 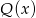 przez wielomian
przez wielomian 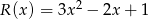 . Oblicz wartości współczynników
. Oblicz wartości współczynników 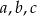 i
i 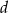 .
.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 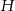 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.
Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.

