/Szkoła średnia/Zadania maturalne/Matura 2015/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 2 czerwca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 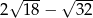 jest równa
jest równa
A) 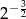 B)
B) 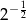 C)
C) 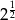 D)
D) 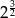
Wartość wyrażenia 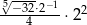 jest równa
jest równa
A) 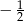 B)
B) 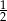 C) 1 D)
C) 1 D) 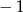
Przy 23-procentowej stawce podatku VAT cena brutto samochodu jest równa 45 018 zł. Jaka jest cena netto tego samochodu?
A) 34 663,86 zł B) 36 600 zł C) 44 995 zł D) 55 372,14 zł
Wyrażenie 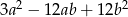 może być przekształcone do postaci
może być przekształcone do postaci
A) 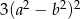 B)
B) 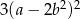 C)
C) 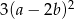 D)
D) 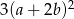
Para liczb 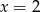 i
i 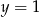 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 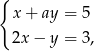 gdy
gdy
A) 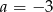 B)
B) 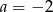 C)
C) 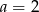 D)
D) 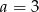
Równanie 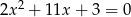
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Wartość wyrażenia 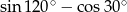 jest równa
jest równa
A) 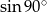 B)
B) 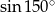 C)
C) 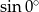 D)
D) 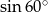
Wyrażenie 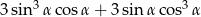 może być przekształcone do postaci
może być przekształcone do postaci
A) 3 B) 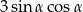 C)
C) 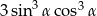 D)
D) 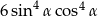
Na rysunku przedstawiony jest fragment prostej o równaniu 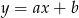 przechodzącej przez punkty
przechodzącej przez punkty 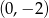 i
i 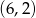 .
.
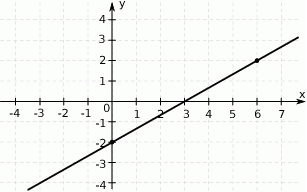
Wtedy
A) 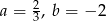 B)
B) 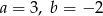 C)
C) 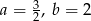 D)
D) 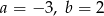
Prosta 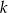 przecina oś
przecina oś 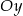 układu współrzędnych w punkcie
układu współrzędnych w punkcie 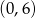 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 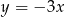 . Wówczas prosta
. Wówczas prosta 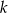 przecina oś
przecina oś 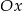 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 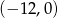 B)
B) 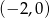 C)
C) 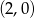 D)
D) 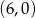
Liczba niewymiernych rozwiązań równania 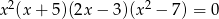 jest równa
jest równa
A) 0 B) 1 C) 5 D) 2
Na rysunku przedstawiono wykres funkcji 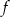 .
.
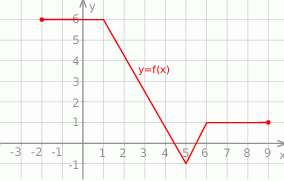
Funkcja 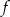 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 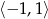 B)
B) 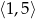 C)
C) 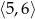 D)
D) 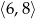
Ciąg geometryczny 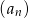 jest określony wzorem
jest określony wzorem 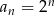 dla
dla 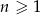 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 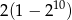 B)
B) 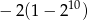 C)
C) 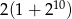 D)
D) 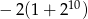
Suma pierwszego i szóstego wyrazu pewnego ciągu arytmetycznego jest równa 13 . Wynika stąd, że suma trzeciego i czwartego wyrazu tego ciągu jest równa
A) 13 B) 12 C) 7 D) 6
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 3:4:5. Najmniejszy kąt wewnętrzny tego trójkąta ma miarę
A) 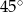 B)
B) 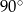 C)
C) 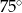 D)
D) 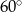
W trójkącie 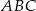 , w którym
, w którym 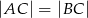 , na boku
, na boku 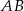 wybrano punkt
wybrano punkt 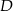 taki, że
taki, że 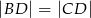 oraz
oraz 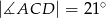 (zobacz rysunek).
(zobacz rysunek).
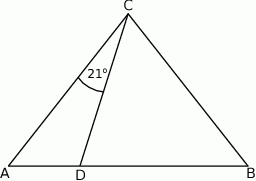
Wynika stąd, że kąt 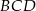 ma miarę
ma miarę
A) 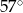 B)
B) 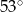 C)
C) 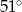 D)
D) 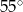
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 7 cm, a drugi ma 2 cm. Trzeci bok tego trójkąta może mieć długość
A) 12 cm B) 9 cm C) 6 cm D) 3 cm
Boki trójkąta mają długości 20 i 12, a kąt między tymi bokami ma miarę  . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 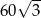 D)
D) 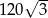
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
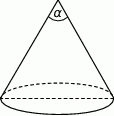
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 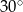 B)
B) 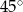 C)
C) 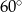 D)
D) 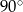
Graniastosłup o podstawie ośmiokąta ma dokładnie
A) 16 wierzchołków. B) 9 wierzchołków. C) 16 krawędzi. D) 8 krawędzi.
W ostrosłupie czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt nachylenia krawędzi bocznej do płaszczyzny podstawy ma miarę
A) 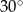 B)
B) 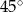 C)
C) 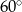 D)
D) 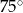
Liczba 0,3 jest jednym z przybliżeń liczby 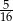 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 4% B) 0,04% C) 2,5% D) 0,025%
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,
, natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  ,
, 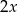 jest równa
jest równa 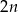 . Wynika stąd, że
. Wynika stąd, że
A) 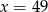 B)
B) 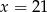 C)
C) 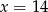 D)
D) 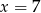
Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 6 B) 10 C) 12 D) 15
Na loterię przygotowano pulę 100 losów, w tym 4 wygrywające. Po wylosowaniu pewnej liczby losów, wśród których był dokładnie jeden wygrywający, szansa na wygraną była taka sama jak przed rozpoczęciem loterii. Stąd wynika, że wylosowano
A) 4 losy. B) 20 losów. C) 50 losów. D) 25 losów.
Zadania otwarte
Rozwiąż nierówność 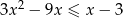 .
.
Rozwiąż równanie 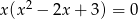 .
.
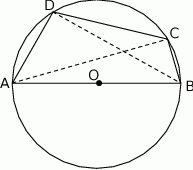
Bok 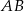 czworokąta
czworokąta 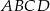 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 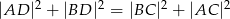 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 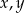 prawdziwa jest nierówność
prawdziwa jest nierówność 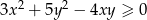 .
.
Funkcja kwadratowa, 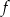 dla
dla 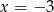 przyjmuje wartość największą równą 4. Do wykresu funkcji
przyjmuje wartość największą równą 4. Do wykresu funkcji 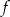 należy punkt
należy punkt 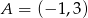 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 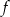 .
.
Ze zbioru liczb naturalnych dwucyfrowych losowo wybieramy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 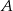 polegającego na tym, że otrzymamy liczbę podzielną przez 8 lub liczbę podzielną przez 12.
polegającego na tym, że otrzymamy liczbę podzielną przez 8 lub liczbę podzielną przez 12.
Dany jest nieskończony rosnący ciąg arytmetyczny 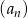 , dla
, dla 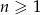 taki, że
taki, że 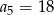 . Wyrazy
. Wyrazy 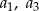 oraz
oraz 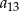 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 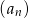 .
.
Dany jest trójkąt równoramienny 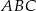 , w którym
, w którym 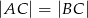 . Ponadto wiadomo, że
. Ponadto wiadomo, że 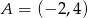 i
i 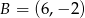 . Wierzchołek
. Wierzchołek 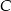 należy do osi
należy do osi 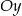 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 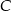 .
.
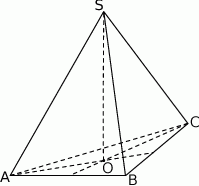
Objętość ostrosłupa prawidłowego trójkątnego 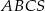 jest równa
jest równa 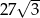 . Długość krawędzi
. Długość krawędzi 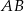 podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.