/Szkoła średnia/Zadania maturalne/Matura 2015/Matura
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 25 sierpnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Jeśli 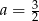 i
i 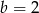 , to wartość wyrażenia
, to wartość wyrażenia 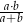 jest równa
jest równa
A) 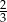 B) 1 C)
B) 1 C)  D)
D) 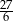
Dany jest prostokąt o wymiarach 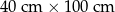 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 8%
B) zwiększy się o 4%
C) zmniejszy się o 8%
D) zmniejszy się o 4%
Liczba 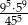 jest równa
jest równa
A) 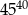 B)
B) 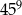 C)
C) 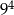 D)
D) 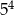
Liczba 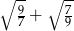 jest równa
jest równa
A) 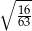 B)
B) 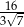 C) 1 D)
C) 1 D) 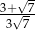
Wartość wyrażenia 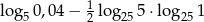 jest równa
jest równa
A) 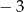 B)
B) 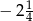 C)
C) 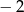 D) 0
D) 0
Wartość wyrażenia 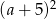 jest większa od wartości wyrażenia
jest większa od wartości wyrażenia 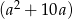 o
o
A) 50 B) 10 C) 5 D) 25
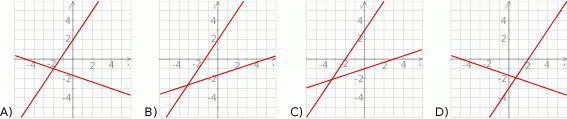
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 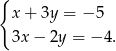 Wskaż ten rysunek
Wskaż ten rysunek
Najmniejszą liczbą całkowitą spełniającą nierówność 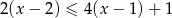 jest
jest
A) 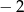 B)
B) 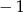 C) 0 D) 1
C) 0 D) 1
Rozwiązaniem równania 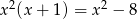 jest
jest
A) 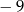 B)
B) 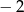 C) 2 D) 7
C) 2 D) 7
Funkcja 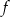 jest określona wzorem
jest określona wzorem 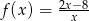 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 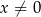 . Wówczas wartość funkcji
. Wówczas wartość funkcji 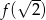 jest równa
jest równa
A) 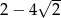 B)
B) 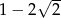 C)
C) 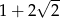 D)
D) 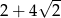
Parabola o wierzchołku 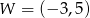 i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A) 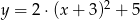
B) 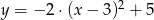
C) 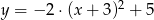
D) 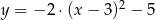
Wykres funkcji liniowej 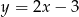 przecina oś
przecina oś  w punkcie o współrzędnych
w punkcie o współrzędnych
A) 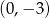 B)
B) 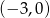 C)
C) 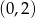 D)
D) 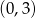
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 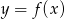 ma współrzędne
ma współrzędne 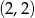 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 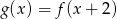 ma współrzędne
ma współrzędne
A) 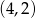 B)
B) 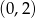 C)
C) 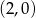 D)
D) 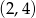
Wszystkie dwucyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba
A) 77 B) 84 C) 91 D) 98
Ciąg liczbowy określony jest wzorem 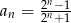 , dla
, dla 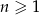 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 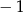 B)
B) 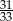 C)
C) 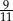 D) 1
D) 1
Sinus kąta ostrego  jest równy
jest równy  . Wówczas
. Wówczas
A) 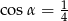 B)
B) 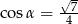 C)
C) 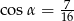 D)
D) 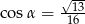
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 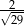 D)
D) 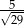
Pole rombu o boku 6 i kącie rozwartym 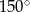 jest równe
jest równe
A) 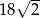 B) 18 C)
B) 18 C) 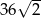 D) 36
D) 36
W okręgu o środku 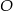 dany jest kąt o mierze
dany jest kąt o mierze 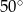 , zaznaczony na rysunku.
, zaznaczony na rysunku.
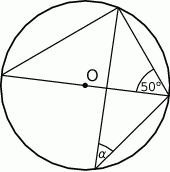
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 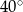 B)
B) 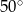 C)
C) 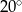 D)
D) 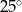
Współczynnik kierunkowy prostej, na której leżą punkty 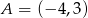 oraz
oraz 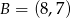 , jest równy
, jest równy
A) 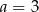 B)
B) 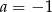 C)
C) 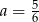 D)
D) 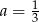
Punkt 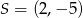 jest środkiem odcinka
jest środkiem odcinka 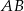 , gdzie
, gdzie 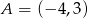 i
i 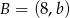 . Wtedy
. Wtedy
A) 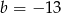 B)
B) 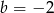 C)
C) 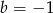 D)
D) 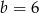
Dany jest trójkąt prostokątny o długościach boków 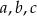 , gdzie
, gdzie 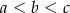 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 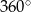 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 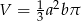 B)
B) 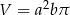 C)
C) 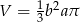 D)
D) 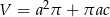
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość
A) 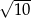 B)
B) 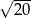 C)
C) 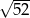 D) 10
D) 10
W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że będzie to kobieta, jest równe
A) 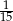 B)
B) 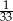 C)
C) 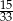 D)
D) 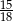
Ile jest wszystkich liczb czterocyfrowych, większych 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 3 B) 6 C) 9 D) 27
Zadania otwarte
Rozwiąż równanie 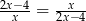 , gdzie
, gdzie 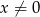 i
i 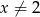 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.
Rozwiąż nierówność 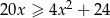 .
.
Kąt  jest ostry i
jest ostry i 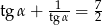 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 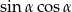 .
.
Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych 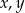 prawdziwa jest nierówność
prawdziwa jest nierówność 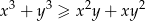 .
.
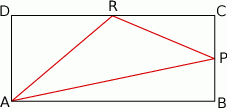
W prostokącie 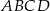 punkt
punkt 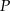 jest środkiem boku
jest środkiem boku 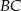 , a punkt
, a punkt 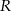 jest środkiem boku
jest środkiem boku 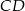 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 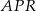 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 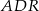 oraz
oraz 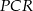 .
.
Wyznacz równanie osi symetrii trójkąta o wierzchołkach 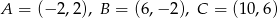 .
.
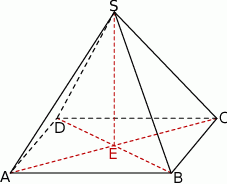
Podstawą ostrosłupa  jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt
jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt  jest wyznaczony przez przecinające się przekątne podstawy, a odcinek
jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 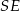 jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem
jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 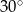 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Funkcja kwadratowa 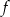 określona jest wzorem
określona jest wzorem 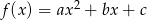 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 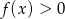 jest przedział
jest przedział 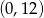 . Największa wartość funkcji
. Największa wartość funkcji 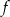 jest równa 9. Oblicz współczynniki
jest równa 9. Oblicz współczynniki 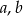 i
i  funkcji
funkcji 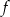 .
.

