/Szkoła średnia/Zadania testowe/Funkcje/Z wartością bezwzględną

Zadanie nr 3276268

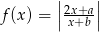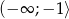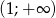Funkcja || 2x+a-|| f(x) = | x+b | jest funkcją malejącą w przedziale (− ∞ ;− 1⟩ oraz (1;+ ∞ ) , rosnącą w przedziale 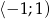⟨−1 ;1) , a do jej wykresu należy punkt 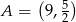A = (9, 5) 2 . Zatem wzór funkcji 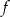f ma postać
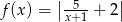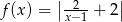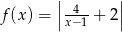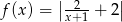
A) | 5 | f(x ) = |x+1-+ 2| B) | 2 | f(x ) = |x−1-+ 2| C) | | f(x ) = ||-4--+ 2|| x−1 D) | | f (x) = |x2+1-+ 2|

Wersja PDF

Rozwiązanie

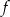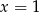Jedyną liczbą, która nie należy do sumy podanych przedziałów monotoniczności funkcji f jest x = 1 , więc właśnie dla tego argumentu musi się zerować mianownik we wzorze funkcji 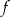f . Zatem 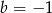b = − 1 i

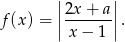
| | f (x) = ||2x-+-a-||. | x− 1 |

Wiemy ponadto, że funkcja zmienia monotoniczność w 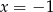x = − 1 , więc dla tego argumentu musi się zerować funkcja homograficzna pod wartością bezwzględną. Zatem 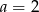a = 2 i

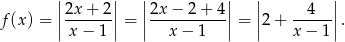
||2x + 2 || ||2x − 2 + 4|| || 4 || f (x) = ||-------|| = ||----------|| = ||2 + ------||. x− 1 x − 1 x − 1

Oczywiście równie dobrze mogliśmy wykorzystać podaną informację o tym, że 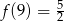f(9 ) = 52 .  
Odpowiedź: C

Wersja PDF