Zadanie nr 5784667
Funkcja 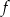 określona jest wzorem
określona jest wzorem 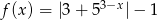 dla każdej liczby rzeczywistej. Zbiorem wartości funkcji
dla każdej liczby rzeczywistej. Zbiorem wartości funkcji 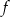 jest
jest
A) 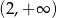 B)
B) 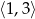 C)
C) 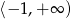 D)
D) 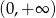
Rozwiązanie
Sposób I
Zbiorem wartości funkcji wykładnicznej postaci 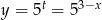 jest przedział
jest przedział 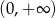 , więc zbiorem wartości wyrażenia
, więc zbiorem wartości wyrażenia 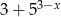 jest przedział
jest przedział 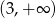 . To oznacza, że zbiorem wartości funkcji
. To oznacza, że zbiorem wartości funkcji 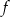 jest przedział
jest przedział 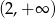 .
.
Sposób II
Szkicujemy wykres funkcji 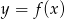 . Rozpoczynamy od wykresu funkcji wykładniczej
. Rozpoczynamy od wykresu funkcji wykładniczej 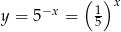 , który przesuwamy o wektor
, który przesuwamy o wektor ![[3,3]](https://img.zadania.info/zad/5784667/HzadR8x.gif) . Potem otrzymany wykres (który jest w całości powyżej osi
. Potem otrzymany wykres (który jest w całości powyżej osi 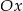 ) przesuwamy o jedną jednostkę w dół.
) przesuwamy o jedną jednostkę w dół.
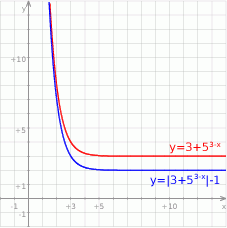
Z wykresu odczytujemy, że zbiorem wartości jest przedział 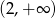 .
.
Sposób III
Zauważmy, że wyrażenie pod wartością bezwzględną we wzorze funkcji 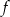 jest zawsze dodatnie, więc
jest zawsze dodatnie, więc
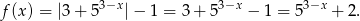
Zbiór wartości wyznaczamy tak samo jak w poprzednich sposobach.
Odpowiedź: A

