Zadanie nr 6037323

Granica 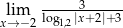-----3------ xl→im−2 log1,2|x+2|+3
A) jest równa 0 B) jest równa 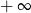+ ∞ C) jest równa 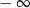− ∞ D) nie istnieje

Rozwiązanie

Sposób I

Ponieważ podstawa logarytmu jest większa od 1, mamy

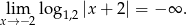
xl→im−2 lo g1,2|x + 2| = − ∞ .

Stąd

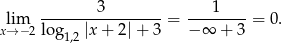
--------3-------- ----1--- lxi→m− 2log |x + 2|+ 3 = − ∞ + 3 = 0. 1,2

Sposób II

Szkicujemy wykres funkcji 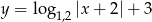y = log |x+ 2|+ 3 1,2 – wykres ten powstaje z wykresu 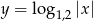y = log1,2 |x | przez przesunięcie o wektor [− 2,3] .

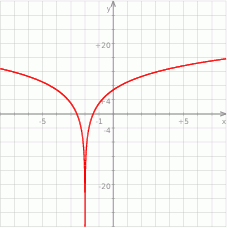
Z wykresu jest jasne, że

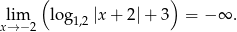
( ) lim lo g1,2|x + 2| + 3 = − ∞ . x→ −2

Stąd

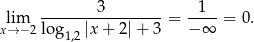
3 1 lim ----------------- = ---- = 0. x→− 2log1,2|x + 2|+ 3 − ∞

Odpowiedź: A

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz