Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 7638676

Funkcja 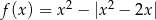2 2 f(x) = x − |x − 2x | określona dla wszystkich liczb rzeczywistych
A) ma trzy miejsca zerowe. B) jest rosnąca.
C) ma jedno minimum lokalne. D) nie ma ekstremów lokalnych.

Wersja PDF
Rozwiązanie

Zapiszmy wzór funkcji 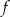f bez użycia wartości bezwzględnej.

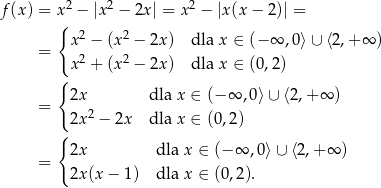
2 2 2 f(x) = x{ − |x − 2x| = x − |x(x − 2)| = x2 − (x2 − 2x ) dla x ∈ (− ∞ ,0⟩∪ ⟨2,+ ∞ ) = 2 2 x + (x − 2x ) dla x ∈ (0,2) { = 2x dla x ∈ (− ∞ ,0⟩∪ ⟨2 ,+ ∞ ) 2x 2 − 2x dla x ∈ (0,2) { 2x dla x ∈ (− ∞ ,0⟩∪ ⟨2 ,+ ∞ ) = 2x (x − 1) dla x ∈ (0,2).

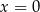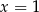Widać teraz gołym okiem, że funkcja ta ma dwa miejsca zerowe: x = 0 i x = 1 . Na przedziale 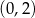(0,2) funkcja jest kawałkiem paraboli o ramionach skierowanych w górę i wierzchołku w 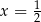x = 1 2 . Nie jest to więc funkcja rosnąca i ma ona minimum w 1 x = 2 .

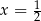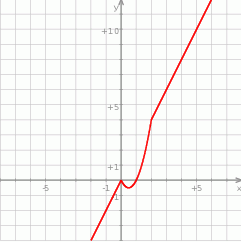
Na koniec dla ciekawskich wykres funkcji 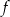f .

PIC

 
Odpowiedź: C

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!