Zadanie nr 8343710
Wiadomo, że funkcja 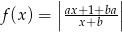 jest funkcją rosnącą w przedziałach
jest funkcją rosnącą w przedziałach 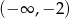 i
i 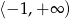 oraz jest funkcją malejącą w przedziale
oraz jest funkcją malejącą w przedziale 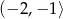 . Zatem
. Zatem
A) 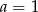 B)
B) 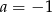 C)
C) 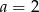 D)
D) 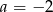
Rozwiązanie
Z informacji podanych w treści zadania wynika, że jedyną liczbą, która nie należy do dziedziny funkcji jest 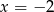 . Zatem
. Zatem 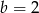 i
i
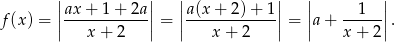
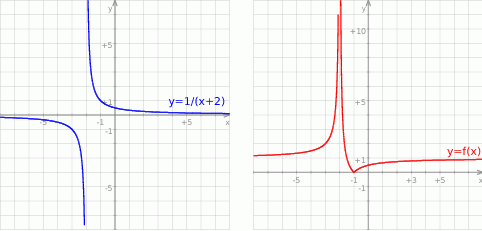
Wykres funkcji 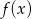 powstaje więc z hiperboli
powstaje więc z hiperboli 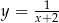 przez przesunięcie o
przez przesunięcie o  w pionie (wzdłuż osi
w pionie (wzdłuż osi 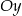 ), a następnie odbicie części wykresu znajdującej się poniżej osi
), a następnie odbicie części wykresu znajdującej się poniżej osi 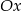 do góry. Jeżeli naszkicujemy tę sytuację to widać, że musi być
do góry. Jeżeli naszkicujemy tę sytuację to widać, że musi być 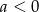 (bo inaczej funkcja byłaby malejąca na lewo od swojego miejsca zerowego) oraz
(bo inaczej funkcja byłaby malejąca na lewo od swojego miejsca zerowego) oraz 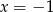 musi być jej miejscem zerowym.
musi być jej miejscem zerowym.
Zatem
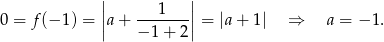
Odpowiedź: B

