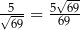/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Różne

Zadanie nr 2677835

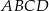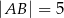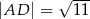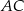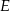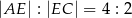W prostokącie ABCD , w którym |AB | = 5 , √ --- |AD | = 11 , na przekątnej AC wybrano taki punkt E , że |AE | : |EC | = 4 : 2 . Oblicz sinus kąta EBC .

Wersja PDF

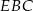Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

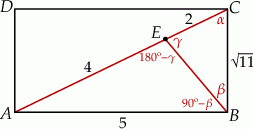
Obliczmy długość przekątnej prostokąta

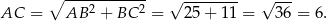
∘ ------------ √ -------- √ --- AC = AB 2 + BC 2 = 25+ 11 = 36 = 6.

Zatem

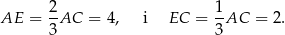
AE = 2AC = 4, i EC = 1AC = 2. 3 3

Sposób I

Stosujemy twierdzenie sinusów w trójkątach EBC i ABE :

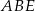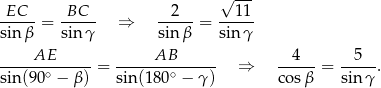
√ --- EC BC 2 11 -----= ----- ⇒ -----= ----- sin β sin γ sin β sinγ ----AE------- -----AB------- --4-- --5-- sin (90∘ − β) = sin(180∘ − γ ) ⇒ cos β = sin γ .

Teraz z obu równości obliczamy 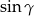sin γ i porównujemy otrzymane wartości.

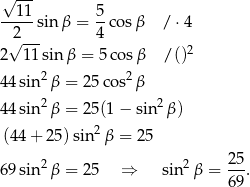
√ --- --11-sinβ = 5-cosβ / ⋅4 √2--- 4 2 11 sin β = 5 cos β / ()2 2 2 44sin β = 25 cos β 44sin2 β = 25 (1 − sin2 β) (44 + 25) sin 2β = 25 25 69sin2 β = 25 ⇒ sin2β = ---. 69

Zatem 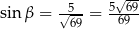--5- 5√-69 sin β = √ 69 = 69 .

Sposób II

Tym razem skorzystamy z twierdzenia cosinusów w trójkącie 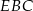EBC .

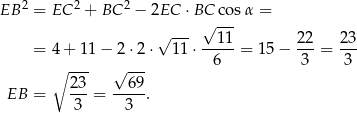
EB 2 = EC 2 + BC 2 − 2EC ⋅BC co sα = √ --- √ --- --11- 22- 23- = 4 + 1 1− 2 ⋅2 ⋅ 11 ⋅ 6 = 15 − 3 = 3 ∘ --- √ --- EB = 23-= --69. 3 3

Teraz korzystamy z twierdzenia sinusów w trójkącie 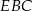EBC .

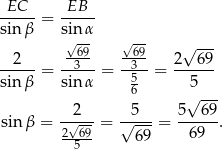
EC EB -----= ----- sin β si√nα √-- 2 -69- -69- 2√ 69- -----= --3-- = --3- = ------ sin β sinα 56 5 √ --- sinβ = -√2--= √-5--= 5--69-. 2--69- 69 69 5

 
Odpowiedź: --5- 5√-69- √ 69 = 69

Wersja PDF