/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Różne

Zadanie nr 9020985

Dany jest prostokąt 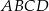ABCD , w którym 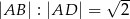√ -- |AB | : |AD | = 2 . Punkt 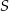S jest środkiem boku 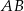AB . Oblicz miarę kąta między prostymi 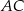AC i DS .

Wersja PDF

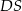Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

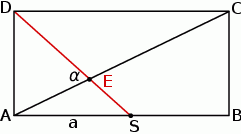
Sposób I

Jeżeli oznaczymy 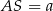AS = a , to

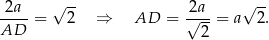
2a √ -- 2a √ -- ----= 2 ⇒ AD = √---= a 2. AD 2

Stąd

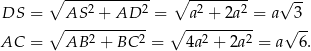
∘ ----2------2 ∘ -2-----2- √ -- DS = ∘ AS---+-AD--- = ∘ -a-+-2a--= a 3 AC = AB 2 + BC 2 = 4a2 + 2a2 = a√ 6.

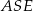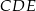Zauważmy, że trójkąty ASE i CDE są podobne (mają równe kąty) oraz znamy ich skalę podobieństwa 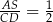AS 1 CD- = 2 . W takim razie

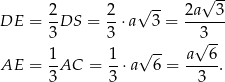
√ -- √ -- DE = 2-DS = 2-⋅a 3 = 2a--3- 3 3 3-- 1 1 √ -- a√ 6 AE = --AC = --⋅a 6 = -----. 3 3 3

Piszemy teraz twierdzenie cosinusów w trójkącie 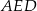AED .

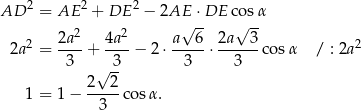
2 2 2 AD = AE + DE − 2AE√ ⋅DE c√os-α 2 2a2 4a2 a 6 2a 3 2 2a = ----+ ---− 2⋅ -----⋅------cos α / : 2a 3 √ -3 3 3 1 = 1− 2--2-cos α. 3

Stąd 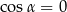co sα = 0 , czyli α = 90∘ .

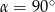Sposób II

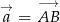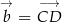Tym razem wykorzystamy podstawowe własności iloczynu skalarnego. Oznaczmy → −→ a = AB i → −→ b = CD . Mamy wtedy

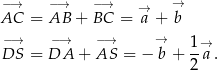
−→ −→ −→ → → AC = AB + BC = a + b −→ −→ −→ → 1 → DS = DA + AS = − b + --a. 2

Stąd

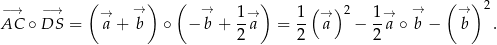
−→ − → ( → ) ( → ) ( )2 → ( → )2 AC ∘DS = →a + b ∘ − b + 1-→a = 1- →a − 1→a ∘ b − b . 2 2 2

Korzystamy teraz z tego, że

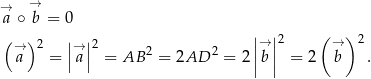
→ → a ∘ b = 0 ( )2 | |2 ||→ ||2 ( → ) 2 →a = ||→a|| = AB 2 = 2AD 2 = 2|b | = 2 b . | |

Mamy zatem

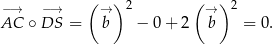
( )2 ( ) 2 −→ −→ → → AC ∘ DS = b − 0 + 2 b = 0.

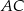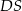To oznacza, że proste AC i DS są prostopadłe.  
Odpowiedź: ∘ 90

Wersja PDF