/Szkoła średnia/Zadania testowe/Funkcje/Wymierna/Granice

Zadanie nr 9569814

Dodaj do ulubionych
Dodaj do rozwiązanych

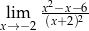
Granica x2−x−6- xl→im−2 (x+2)2
A) nie istnieje B) jest równa 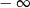− ∞ C) jest liczbą rzeczywistą D) jest równa + ∞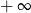

Rozwiązanie

Łatwo sprawdzić, że licznik zeruje się dla 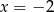x = − 2 , więc jest to jeden z pierwiastków licznika. Drugi pierwiastek możemy wyznaczyć np. ze wzorów Vièta’a.

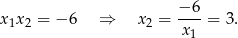
x x = − 6 ⇒ x = −-6-= 3. 1 2 2 x 1

Mamy zatem

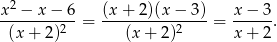
x2-−-x-−-6- (x-+-2)(x-−-3)- x-−-3- (x + 2)2 = (x + 2)2 = x + 2.

Liczymy granice jednostronne

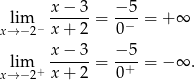
x−--3- −5-- xl→im−2− x+ 2 = 0− = + ∞ lim x−--3-= −5-= − ∞ . x→ −2+ x+ 2 0+

Granice jednostronne są różne, więc interesująca nas granica nie istnieje.

Na koniec wykres dla ciekawskich.

PIC

 
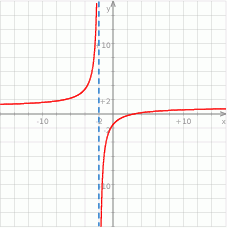
Odpowiedź: A

Wersja PDF