Zadanie nr 3141582
Styczna do wykresu funkcji 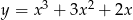 w punkcie
w punkcie 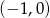 ma równanie
ma równanie
A) 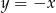 B)
B) 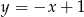 C)
C) 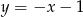 D)
D) 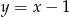
Rozwiązanie
Liczymy pochodną
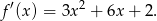
Współczynnik kierunkowy interesującej nas stycznej jest równy
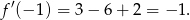
Styczna ma więc równanie postaci 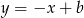 . Ponieważ
. Ponieważ 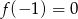 , mamy
, mamy 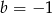 . Na koniec obrazek dla ciekawskich.
. Na koniec obrazek dla ciekawskich.
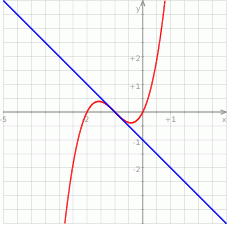
Odpowiedź: C

