Zadanie nr 9567798
Funkcja określona dla każdej liczby rzeczywistej 
wzorem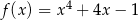 
A) ma więcej niż dwa minima lokalne. B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne. D) nie ma minimum lokalnego.
Rozwiązanie
Liczymy pochodną funkcji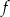 
.
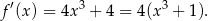
Pochodna ma dokładnie jedno miejsce zerowe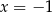 
i przechodząc przez ten punkt zmienia znak z ujemnego na dodatni. To oznacza, że funkcja 
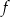ma w tym punkcie minimum lokalne i jest to jedyne ekstermum lokalne tej funkcji.
Odpowiedź: C
