/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Rekurencyjny

Zadanie nr 4715577

Ciąg 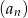(an ) określony jest w następujący sposób 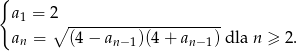{ a 1 = 2∘ --------------------- an = (4 − an− 1)(4+ an −1) dla n ≥ 2. Setny wyraz ciągu 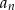a n jest równy
A) 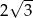√ -- 2 3 B) 2 C) 100 D)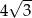 √ -- 4 3

Wersja PDF

Rozwiązanie

Zapiszmy wzór ciągu w postaci

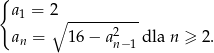
{ a1 = 2∘ ---------- an = 16− a2 dla n ≥ 2. n−1

Sposób I

Liczymy

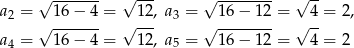
a = √ 16-−-4-= √ 1-2, a = √ 16−--12-= √ 4-= 2 , 2 √ ------- √ --- 3 √ -------- √ -- a4 = 16 − 4 = 1 2, a5 = 16− 12 = 4 = 2

i tak dalej. Widać stąd, że 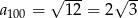√ --- -- a = 12 = 2√ 3 100 .

Sposób II

Zauważmy, że

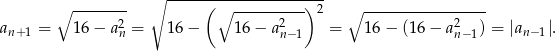
∘ ---------------------- ∘ -------- (∘ ---------) 2 ∘ ----------------- an+1 = 16 − a2n = 16− 16 − a2n−1 = 16− (16− a2n−1) = |an− 1|.

Wiemy ponadto, że 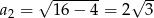√ ------- √ -- a2 = 16 − 4 = 2 3 , więc

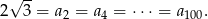
√ -- 2 3 = a2 = a 4 = ⋅⋅⋅ = a100.

 
Odpowiedź: A

Wersja PDF