Zadanie nr 5936878
Ciąg 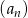 dla każdego
dla każdego 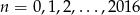 spełnia warunek
spełnia warunek 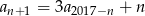 . Wyraz
. Wyraz 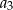 tego ciągu jest równy
tego ciągu jest równy
A) 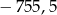 B)
B) 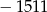 C)
C) 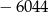 D)
D) 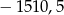
Rozwiązanie
Podstawiamy w danym wzorze rekurencyjnym 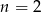 , a potem
, a potem 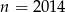 .
.
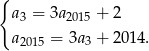
Podstawiamy teraz z drugiego równania do pierwszego.
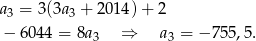
Odpowiedź: A

