/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Rekurencyjny

Zadanie nr 7320224

Ciąg 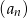(an ) określony jest wzorem rekurencyjnym 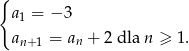{ a1 = − 3 an+1 = an + 2 dla n ≥ 1. Wówczas wzór ogólny ciągu 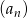(a ) n ma postać
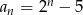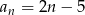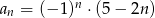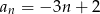
A) n an = 2 − 5 B) an = 2n − 5 C) an = (− 1)n ⋅(5 − 2n) D) an = − 3n + 2

Wersja PDF

Rozwiązanie

Sposób I

Liczymy

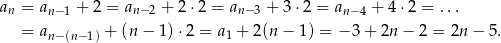
a = a + 2 = a + 2 ⋅2 = a + 3 ⋅2 = a + 4⋅2 = ... n n− 1 n−2 n− 3 n− 4 = an− (n− 1) + (n − 1) ⋅2 = a 1 + 2(n − 1) = − 3+ 2n − 2 = 2n − 5.

Sposób II

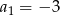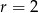Z podanego określenia ciągu powinno być jasne, że mamy do czynienia z ciągiem arytmetycznym, w którym a1 = − 3 i r = 2 . Mamy zatem

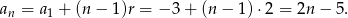
an = a1 + (n − 1)r = − 3+ (n− 1)⋅2 = 2n − 5.

 
Odpowiedź: B

Wersja PDF