Zadanie nr 4358085
W trójkącie 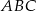 długość środkowej
długość środkowej 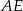 jest równa połowie długości boku
jest równa połowie długości boku 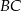 . Wówczas trójkąt
. Wówczas trójkąt 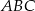 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
Rozwiązanie
Zaczynamy od rysunku
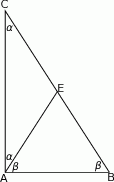
Sposób I
Ponieważ 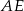 jest środkową, więc
jest środkową, więc 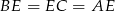 . Zatem trójkąty
. Zatem trójkąty 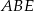 i
i 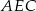 są równoramienne, czyli
są równoramienne, czyli
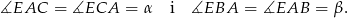
Liczymy teraz sumę miar kątów w trójkącie 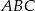 .
.
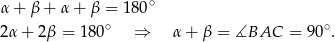
Zatem trójkąt jest prostokątny.
Sposób II
Ponieważ 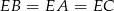 , punkt
, punkt 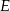 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 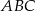 . To jednak oznacza, że kąt
. To jednak oznacza, że kąt 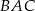 jest oparty na średnicy, czyli jest prosty.
jest oparty na średnicy, czyli jest prosty.
Odpowiedź: B

