Zadanie nr 5641277
Jeżeli środek okręgu opisanego na trójkącie leży na wysokości trójkąta, to trójkąt ten musi być
A) równoboczny B) równoramienny C) prostokątny D) rozwartokątny
Rozwiązanie
Środek okręgu opisanego to punkt przecięcia się symetralnych jego boków.
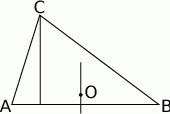
Skoro leży on na wysokości, powiedzmy opuszczonej na bok 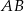 , to symetralna boku
, to symetralna boku 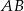 i ta wysokość muszą się pokrywać (bo obie proste są prostopadłe do
i ta wysokość muszą się pokrywać (bo obie proste są prostopadłe do 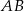 i przechodzą przez
i przechodzą przez 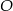 ). Trójkąt, w którym wysokość jest jednocześnie symetralną boku jest trójkątem równoramiennym.
). Trójkąt, w którym wysokość jest jednocześnie symetralną boku jest trójkątem równoramiennym.
Odpowiedź: B

