/Szkoła średnia/Zadania testowe/Kombinatoryka/Zbiory liczb/Podzielność

Zadanie nr 6130725

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczb naturalnych sześciocyfrowych podzielnych przez 5, których cyfra setek należy do zbioru 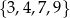{3,4,7,9 } i wszystkie cyfry są różne jest
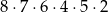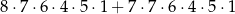
A) 8 ⋅7⋅ 6⋅4 ⋅5 ⋅2 B) 8⋅ 7⋅6 ⋅4 ⋅5⋅ 1+ 7⋅7 ⋅6 ⋅4⋅ 5⋅1
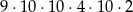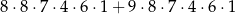
C) 9 ⋅10 ⋅10 ⋅4⋅ 10⋅2 D) 8 ⋅8 ⋅7⋅4 ⋅6 ⋅1 + 9 ⋅8⋅7 ⋅4 ⋅6 ⋅1

Rozwiązanie

Cyfrą jedności utworzonej liczby musi być 0 lub 5.

Jeżeli cyfrą jedności jest 0, to na 4 sposoby wybieramy liczbę setek i na

8 ⋅7 ⋅6⋅ 5

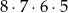
sposobów wybieramy pozostałe cyfry.

Jeżeli cyfrą jedności jest 5, to jest podobnie, ale możliwości wyboru pierwszej cyfry (setek tysięcy jest mniej, bo nie może tam być zero. Pozostałe cztery cyfry możemy więc w tym przypadku wybrać na

7 ⋅7 ⋅6⋅ 5

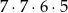
sposobów. W sumie jest więc

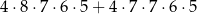
4 ⋅8 ⋅7 ⋅6⋅5 + 4 ⋅7 ⋅7⋅ 6⋅5

liczb spełniających warunki zadania.  
Odpowiedź: B

Wersja PDF