Zadanie nr 6829588
Ile można utworzyć liczb trzycyfrowych podzielnych przez 5, o różnych cyfrach należących do zbioru 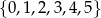 ?
?
A) 40 B) 36 C) 32 D) 28
Rozwiązanie
Liczba jest podzielna przez 5 jeżeli jej cyfra jedności jest równa 0 lub 5.
Zastanówmy się ile możemy utworzyć liczb podzielnych przez 5 jeżeli ustalimy, że cyfrą jedności jest 0. Wówczas cyfrą setek i dziesiątek może być dowolna cyfra ze zbioru 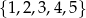 , ale pamiętamy, że cyfry muszą być różne. Zatem możemy utworzyć
, ale pamiętamy, że cyfry muszą być różne. Zatem możemy utworzyć
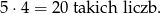
Teraz załóżmy, że cyfrą jedności jest 5. Wówczas cyfrę setek możemy wybrać ze zbioru 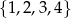 , a cyfrę dziesiątek ze zbioru
, a cyfrę dziesiątek ze zbioru 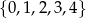 . Zatem możemy utworzyć
. Zatem możemy utworzyć
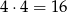
(ponieważ cyfry setek i dziesiątek muszą być różne).
Zatem łącznie możemy utworzyć
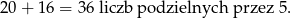
Odpowiedź: B

