Zadanie nr 9756625
Wszystkich par 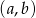 takich, że
takich, że 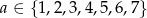 ,
, 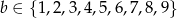 oraz suma
oraz suma 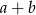 jest podzielna przez 3, jest
jest podzielna przez 3, jest
A) mniej niż 21 B) dokładnie 21 C) dokładnie 22 D) więcej niż 22
Rozwiązanie
Jeżeli z pierwszego zbioru wybierzemy liczbę podzielną przez 3, czyli 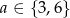 , to z drugiego zbioru też musimy wybrać liczbę podzielną przez 3, czyli
, to z drugiego zbioru też musimy wybrać liczbę podzielną przez 3, czyli 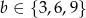 . Jest
. Jest 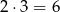 takich par.
takich par.
Jeżeli z pierwszego zbioru wybierzemy liczbę, która daje resztę 1 przy dzieleniu przez 3, czyli 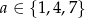 , to z drugiego zbioru musimy wybrać liczbę, która daje resztę 2 przy dzieleniu przez 3, czyli
, to z drugiego zbioru musimy wybrać liczbę, która daje resztę 2 przy dzieleniu przez 3, czyli 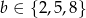 . Takich par jest
. Takich par jest 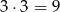 .
.
Jeżeli z pierwszego zbioru wybierzemy liczbę, która daje resztę 2 przy dzieleniu przez 3, czyli 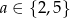 , to z drugiego zbioru musimy wybrać liczbę, która daje resztę 1 przy dzieleniu przez 3, czyli
, to z drugiego zbioru musimy wybrać liczbę, która daje resztę 1 przy dzieleniu przez 3, czyli 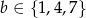 . Takich par jest
. Takich par jest 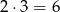 .
.
W sumie jest więc
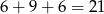
par spełniających warunki zadania.
Odpowiedź: B

