/Szkoła średnia/Ciągi/Granice ciągów/Z parametrem

Zadanie nr 2864408

Dodaj do ulubionych
Dodaj do rozwiązanych

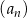Ciąg (an) jest określony dla każdej liczby naturalnej 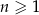n ≥ 1 wzorem

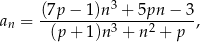
3 an = (7p-−-1)n--+-5pn-−--3, (p + 1)n 3 + n 2 + p

gdzie 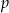p jest liczbą rzeczywistą dodatnią. Oblicz wartość 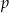p , dla której granica ciągu 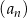(an) jest równa 4 3 .

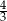Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.