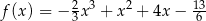/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu

Zadanie nr 3794420

Dodaj do ulubionych
Dodaj do rozwiązanych

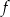Funkcja f jest wielomianem stopnia 3, a jej wykres jest styczny do prostej 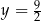y = 92 w punkcie o odciętej 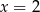x = 2 oraz jest styczny do prostej 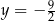y = − 92 w punkcie o odciętej 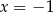x = −1 . Wyznacz wzór funkcji f .

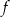Rozwiązanie

Szukamy funkcji 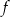f w postaci

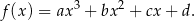
3 2 f(x) = ax + bx + cx+ d.

Jej pochodna jest równa

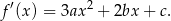
′ 2 f (x) = 3ax + 2bx + c.

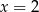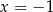Wiemy, że styczne do wykresu są poziome w punktach x = 2 i x = − 1 , więc pochodna zeruje się w tych punktach.

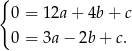
{ 0 = 12a + 4b + c 0 = 3a− 2b+ c.

Odejmujemy od pierwszego równania drugie i mamy

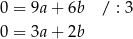
0 = 9a + 6b / : 3 0 = 3a + 2b

Podstawiamy teraz 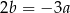2b = − 3a w drugim równaniu układu i mamy

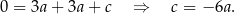
0 = 3a + 3a + c ⇒ c = − 6a .

Wzór funkcji 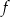f ma więc postać

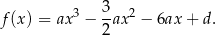
3 3 2 f(x ) = ax − 2-ax − 6ax + d.

Wiemy jeszcze, że wykres tej funkcji przechodzi przez punkty 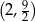( ) 2, 9 2 i ( 9) − 1,− 2 .

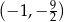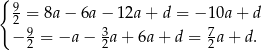
{ 9 2 = 8a − 6a − 12a + d = −1 0a+ d − 92 = −a − 32a + 6a + d = 72a+ d.

Odejmujemy od drugiego równania pierwsze i mamy

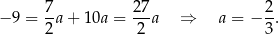
7- 27- 2- − 9 = 2a + 1 0a = 2 a ⇒ a = − 3 .

Stąd

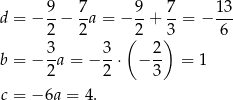
d = − 9-− 7a = − 9+ 7-= − 13- 2 2 2 3 6 3 3 ( 2) b = − --a = − --⋅ − -- = 1 2 2 3 c = − 6a = 4.

i

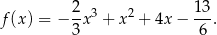
2 13 f(x ) = − -x 3 + x 2 + 4x −--. 3 6

Na koniec wykres funkcji 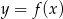y = f (x) .

PIC

 
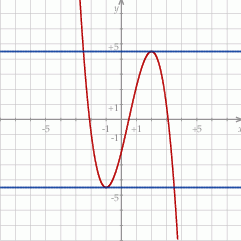
Odpowiedź: f(x ) = − 23x3 + x2 + 4x − 136-

Wersja PDF