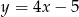/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu

Zadanie nr 9710523

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest parabola o równaniu 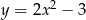2 y = 2x − 3 i leżący na niej punkt 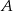A o współrzędnej x równej 1. Wyznacz równanie stycznej do tej paraboli w punkcie A .

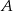Rozwiązanie

Korzystamy z równania stycznej do wykresu funkcji 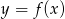y = f(x ) w punkcie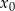 x 0

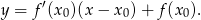
y = f′(x0)(x− x0)+ f(x0).

Liczymy

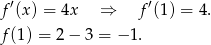
′ ′ f(x ) = 4x ⇒ f (1) = 4. f(1) = 2 − 3 = − 1.

Zatem równanie stycznej ma postać

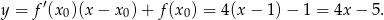
′ y = f (x0)(x − x0) + f (x 0) = 4(x − 1) − 1 = 4x − 5 .

Na koniec obrazek.

PIC

 
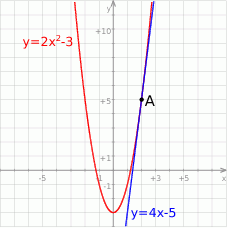
Odpowiedź: y = 4x− 5

Wersja PDF