Zadanie nr 4364330
Oblicz najmniejszą wartość wielomianu 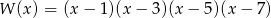 .
.
Rozwiązanie
Sposób I
Spróbujemy zadanie rozwiązać tradycyjnie, czyli z pochodnych. Mamy
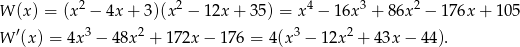
Musimy teraz znaleźć pierwiastki pochodnej. sprawdzamy oczywiście dzielniki wyrazu wolnego. Po jakiejś chwili można zauważyć, że 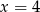 jest pierwiastkiem. Dzielimy zatem przez
jest pierwiastkiem. Dzielimy zatem przez 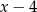 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
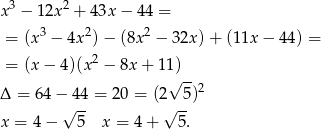
Ponieważ
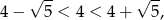
to minima funkcji są przyjmowane w punktach 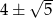 . Policzmy wartości funkcji w tych punktach.
. Policzmy wartości funkcji w tych punktach.
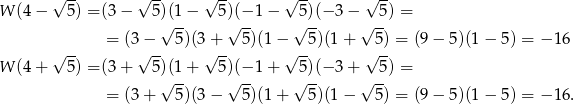
Zatem najmniejsza wartość funkcji to 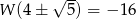 .
.
Sposób II
Zadanie można rozwiązać znacznie prościej korzystając z symetrii danej funkcji względem prostej 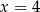 . Ta symetria jest widoczna ze wzoru oraz narzuca się w poprzednim rozwiązaniu. Jeżeli podstawimy
. Ta symetria jest widoczna ze wzoru oraz narzuca się w poprzednim rozwiązaniu. Jeżeli podstawimy 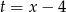 to mamy funkcje
to mamy funkcje
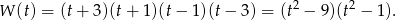
Jest to funkcja dwukwadratowa, więc podstawmy 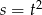 . Mamy wtedy parabolę
. Mamy wtedy parabolę
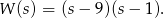
Szukamy najmniejszej wartości tej paraboli dla 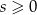 (bo
(bo 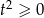 ). Ponieważ jej ramiona są skierowane do góry i wierzchołek jest w punkcie
). Ponieważ jej ramiona są skierowane do góry i wierzchołek jest w punkcie 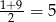 , więc wartość najmniejsza jest przyjmowana dla
, więc wartość najmniejsza jest przyjmowana dla 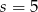 i wynosi ona
i wynosi ona 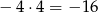 . Śledząc zrobione podstawienia jest jasne, że jest to punkt
. Śledząc zrobione podstawienia jest jasne, że jest to punkt 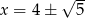 dla oryginalnej funkcji.
dla oryginalnej funkcji.
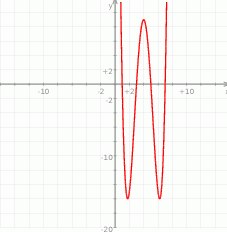
Na koniec, dla ciekawskich, wykres wielomianu 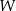 .
.
Odpowiedź: