/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności

Zadanie nr 5964377

Wyznacz te argumenty, dla których funkcja 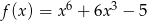6 3 f(x) = x + 6x − 5 osiąga wartość najmniejszą.

Wersja PDF

Rozwiązanie

Sposób I

Podstawmy 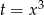3 t = x .

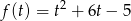
2 f(t) = t + 6t− 5

Wykresem tej funkcji jest parabola o ramionach skierowanych do góry i wierzchołku w punkcie 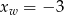xw = − 3 . Zatem wyjściowa funkcja osiąga wartość najmniejszą w punkcie 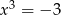x3 = − 3 , czyli dla -- x = − √33 .

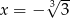Sposób II

Zadanie możemy też łatwo rozwiązać jeżeli nie boimy się pochodnych. Liczymy

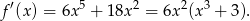
f′(x) = 6x 5 + 18x 2 = 6x2(x 3 + 3 ).

Widać teraz, że pochodna jest ujemna dla 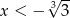x < − √33- (czyli funkcja jest malejąca) oraz jest dodatnia dla 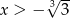√3-- x > − 3 (czyli funkcja jest rosnąca). Zatem w punkcie 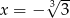√ -- x = − 33 jest globalne minimum funkcji y = f(x ) .

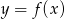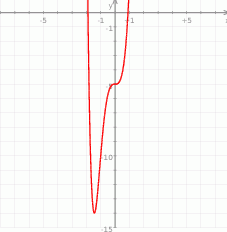
Na koniec, dla ciekawskich, wykres funkcji f(x) .

PIC

 
Odpowiedź: √ -- x = − 3 3

Wersja PDF