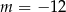Zadanie nr 7812277
Wyznacz wszystkie wartości parametru 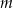 , dla których funkcja
, dla których funkcja 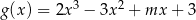 ma ekstremum lokalne równe 10.
ma ekstremum lokalne równe 10.
Rozwiązanie
Liczymy pochodną danej funkcji.
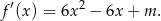
Jeżeli  jest punktem, w którym funkcja ma ekstremum równe 10, to
jest punktem, w którym funkcja ma ekstremum równe 10, to 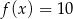 i
i 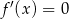 . Otrzymujemy więc układ równań
. Otrzymujemy więc układ równań
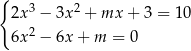
Odejmujemy od pierwszego równania drugie pomnożone przez  i mamy
i mamy
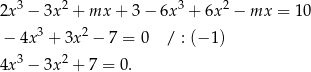
Łatwo zauważyć, że jednym z pierwiastków tego równania jest 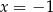 . Dzielimy więc wielomian z lewej strony przez
. Dzielimy więc wielomian z lewej strony przez 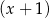 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
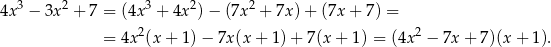
Trójmian w nawiasie nie ma pierwiastków (bo 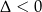 ), więc jedynym rozwiązaniem tego równania jest
), więc jedynym rozwiązaniem tego równania jest 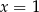 . Mamy wtedy
. Mamy wtedy
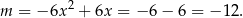
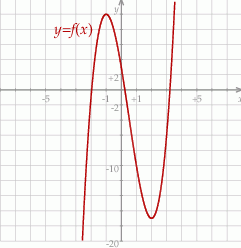
Łatwo sprawdzić, że dla tej wartości 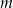 funkcja
funkcja 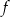 rzeczywiście ma dla argumentu
rzeczywiście ma dla argumentu 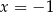 maksimum lokalne równe 10.
maksimum lokalne równe 10.
Odpowiedź: