/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności

Zadanie nr 9052709

Dla jakiej wartości parametru 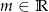m ∈ R funkcja 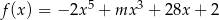5 3 f(x ) = − 2x + mx + 28x + 2 ma ekstremum w punkcie x = 2 ?

Wersja PDF

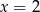Rozwiązanie

Liczymy pochodną danej funkcji.

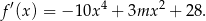
′ 4 2 f (x) = − 10x + 3mx + 28 .

Sprawdzamy teraz dla jakiej wartości 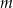m liczba 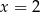x = 2 jest pierwiastkiem pochodnej.

0 = − 160 + 12m + 28 ⇒ 1 2m = 132 ⇒ m = 1 1.

Stąd

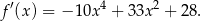
f′(x) = − 1 0x4 + 33x2 + 28.

Powinniśmy jeszcze sprawdzić, że pochodna zmienia znak w punkcie 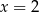x = 2 .

Sposób I

Rozkładamy 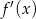f ′(x) na czynniki. W tym celu podstawiamy t = x2 .

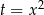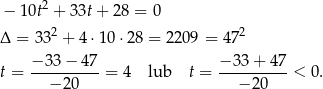
2 − 1 0t + 33t + 28 = 0 Δ = 3 32 + 4⋅10 ⋅28 = 2209 = 4 72 t = −-33-−-47-= 4 lub t = −-33+--47-< 0. − 2 0 − 20

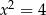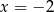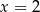Mamy zatem 2 x = 4 , czyli x = − 2 lub x = 2 . To oznacza, że 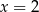x = 2 nie jest pierwiastkiem wielokrotnym 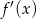f′(x) , więc rzeczywiście funkcja 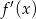f ′(x ) zmienia znak przechodząc przez x = 2 .

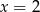Sposób II

Liczymy drugą pochodną

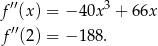
′′ 3 f (x) = − 40x + 66x f ′′(2) = − 188.

To oznacza, że funkcja 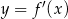′ y = f (x ) jest malejąca w otoczeniu 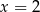x = 2 , czyli rzeczywiście pochodna 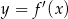′ y = f (x) zmienia znak przy przejściu przez x = 2 .  
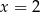Odpowiedź: m = 11

Wersja PDF