/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności/Ekstrema

Zadanie nr 8419432

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla każdej liczby rzeczywistej x obliczamy różnicę sześcianów liczb: o 1 mniejszej od x oraz o 2 większej od x . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.

Rozwiązanie

Nasza funkcja to

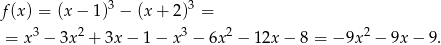
3 3 f(x) = (x − 1) − (x + 2 ) = = x3 − 3x2 + 3x − 1 − x 3 − 6x 2 − 1 2x− 8 = − 9x2 − 9x − 9 .

Wartość największa to wartość w wierzchołku tej paraboli, czyli w punkcie

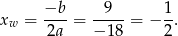
−b 9 1 xw = 2a--= −-1-8 = − 2-.

Liczymy teraz wartość największą.

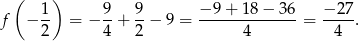
( ) 1 9 9 −9 + 1 8− 36 − 27 f − 2- = − 4-+ 2-− 9 = ------4-------= --4--.

 
Odpowiedź: 2 1 −27 f(x ) = − 9x − 9x − 9, fmax = f(− 2) = -4--

Wersja PDF