/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności/Monotoniczność

Zadanie nr 2377478

Dodaj do ulubionych
Dodaj do rozwiązanych

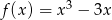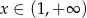Dana jest funkcja 3 f(x ) = x − 3x dla x ∈ (1,+ ∞ ) . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale (1,+ ∞ ) .

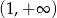Rozwiązanie

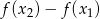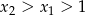Musimy ustalić jaki jest znak wyrażenia f (x2)− f (x1) dla x 2 > x1 > 1 – jeżeli wyrażenie to jest dodatnie to funkcja jest rosnąca, a jeżeli ujemne to jest malejąca.

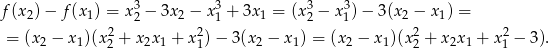
f(x2) − f(x 1) = x32 − 3x2 − x31 + 3x1 = (x 32 − x 31)− 3(x 2 − x 1) = 2 2 2 2 = (x2 − x1)(x2 + x2x 1 + x 1)− 3(x 2 − x 1) = (x2 − x1)(x2 + x2x1 + x1 − 3).

Ponieważ 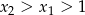x 2 > x1 > 1 obydwa nawiasy są dodatnie.  
Odpowiedź: Funkcja jest rosnąca.

Wersja PDF