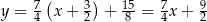/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

Zadanie nr 3580118

Dodaj do ulubionych
Dodaj do rozwiązanych

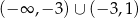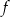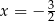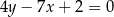Funkcja f jest wielomianem stopnia 3, a jej wykres znajduje się powyżej osi Ox na zbiorze (− ∞ ,− 3)∪ (− 3,1 ) . Wyznacz równanie stycznej do wykresu funkcji f w punkcie x = − 32 jeżeli wiadomo, że styczna ta jest równoległa do prostej 4y− 7x + 2 = 0 .

Rozwiązanie

Jeżeli 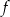f jest wielomianem stopnia 3 i rozwiązaniem nierówności

f(x) > 0

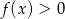
jest zbiór

(− ∞ ,− 3)∪ (− 3,1),

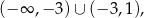
to 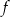f musi mieć postać

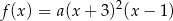
f(x) = a(x+ 3)2(x − 1)

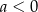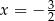dla pewnego a < 0 . Współczynnik a wyznaczymy z podanego kierunku stycznej w punkcie x = − 3 2 . Obliczmy najpierw pochodną funkcji 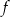f – możemy to zrobić wymnażając najpierw nawiasy we wzorze 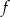f , ale możemy też to zrobić korzystając ze wzoru

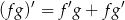
′ ′ ′ (f g) = fg + fg

na pochodną iloczynu. Mamy zatem

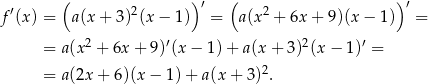
′ ( 2 )′ ( 2 )′ f (x ) = a(x + 3 )(x − 1 ) = a(x + 6x + 9)(x− 1) = 2 ′ 2 ′ = a(x + 6x + 9) (x − 1)+ a(x + 3) (x − 1) = = a(2x + 6)(x − 1) + a(x + 3)2.

Łatwo teraz obliczyć a .

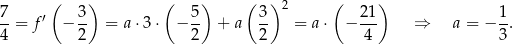
( ) ( ) ( ) 2 ( ) 7- ′ 3- 5- 3- 21- 1- 4 = f − 2 = a⋅3 ⋅ − 2 + a 2 = a⋅ − 4 ⇒ a = − 3 .

Stąd

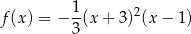
f(x) = − 1(x + 3)2(x − 1) 3

i

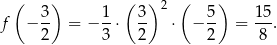
( ) ( ) 2 ( ) f − 3- = − 1-⋅ 3- ⋅ − 5- = 15. 2 3 2 2 8

Styczna w punkcie 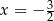x = − 32 ma więc równanie

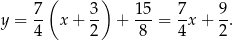
7( 3 ) 1 5 7 9 y = -- x + -- + --- = --x+ -. 4 2 8 4 2

Na koniec wykres funkcji y = f (x) .

PIC

 
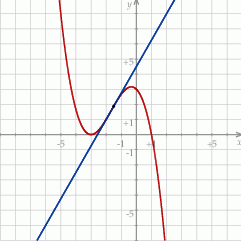
Odpowiedź: ( ) y = 74 x + 32 + 185= 74x + 92

Wersja PDF