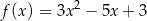/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

Zadanie nr 5771848

Dodaj do ulubionych
Dodaj do rozwiązanych

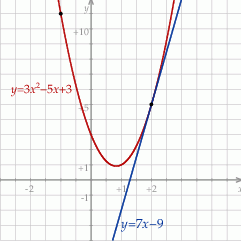
Wyznacz wzór funkcji kwadratowej 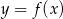y = f(x) wiedząc, że jest on styczny do prostej 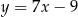y = 7x − 9 w punkcie 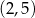(2,5) oraz przechodzi przez punkt (− 1,11 ) .

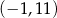Rozwiązanie

Szukamy funkcji w postaci 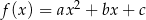2 f(x ) = ax + bx + c . Liczymy pochodną tej funkcji

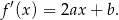
f′(x) = 2ax + b .

Wiemy, że styczna do wykresu w punkcie 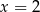x = 2 ma współczynnik kierunkowy równy 7, więc

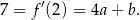
7 = f′(2) = 4a + b.

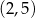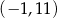Znamy dodatkowo dwa punkty na wykresie: (2,5) i (− 1,11) , co prowadzi do układu równań

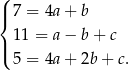
( |{ 7 = 4a + b 11 = a − b + c |( 5 = 4a + 2b + c.

Odejmujemy od trzeciego równania drugie i mamy

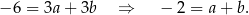
− 6 = 3a + 3b ⇒ − 2 = a+ b .

Odejmujemy tę równość od pierwszego równania i mamy

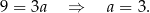
9 = 3a ⇒ a = 3.

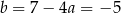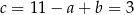Stąd b = 7 − 4a = −5 i c = 11− a+ b = 3 .

PIC

 
Odpowiedź: f (x) = 3x2 − 5x + 3

Wersja PDF