/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

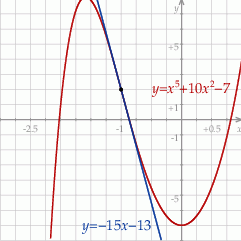
Zadanie nr 6847775

Dodaj do ulubionych
Dodaj do rozwiązanych

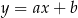Prosta y = ax+ b jest styczna do wykresu funkcji 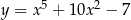5 2 y = x + 10x − 7 . Wykaż, że a ≥ − 15 .

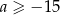Rozwiązanie

Współczynnik kierunkowy stycznej do wykresu w punkcie 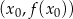(x0,f(x0)) to dokładnie 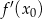f′(x0) . Musimy zatem wykazać, że pochodna

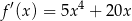
f′(x) = 5x 4 + 2 0x

nie przyjmuje wartości mniejszej niż 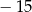− 15 . W tym celu liczymy pochodną z pochodnej

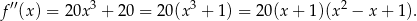
f ′′(x) = 20x 3 + 2 0 = 20(x3 + 1) = 2 0(x+ 1)(x2 − x + 1).

Widać teraz, że druga pochodna 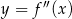y = f′′(x ) jest ujemna w przedziale 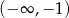(− ∞ ,− 1) i dodatnia w przedziale 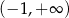(− 1,+ ∞ ) . To oznacza, że pochodna 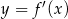′ y = f (x) maleje w przedziale 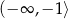(− ∞ ,− 1⟩ i rośnie w przedziale 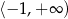⟨−1 ,+∞ ) . W takim razie najmniejsza wartość funkcji y = f ′(x ) to

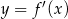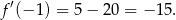
f′(− 1) = 5 − 20 = − 15 .

To oznacza, że faktycznie 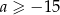a ≥ − 15 .

PIC

Wersja PDF