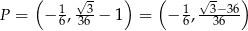/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

Zadanie nr 6989795

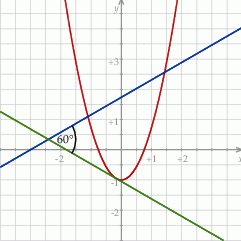
Styczna do paraboli o równaniu 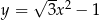√ -- 2 y = 3x − 1 w punkcie 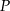P przecina prostą o równaniu 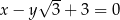√ -- x− y 3 + 3 = 0 pod kątem 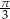π3- . Oblicz współrzędne punktu P .

Wersja PDF

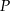Rozwiązanie

Przekształćmy dane równanie prostej, żeby zobaczyć jaki ma ona współczynnik kierunkowy.

√ -- √ -- y 3 = x + 3 / : 3 1 3 √ 3- √ -- π √ -- y = √--x + √---= ----x+ 3 = tg --⋅x + 3. 3 3 3 6

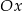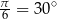To oznacza, że prosta ta tworzy z osią Ox kąt π6-= 30 ∘ . Spróbujmy teraz ustalić, co to oznacza dla stycznej, o której mowa w treści zadania.

PIC

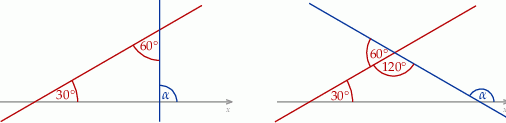
Jeżeli to naszkicujemy to widać, że są dwa możliwe położenia stycznej względem danej prostej (bo nie wiemy, który dokładnie kąt jest równy 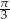π3- ). W pierwszym położeniu styczna jest prostopadła do osi 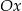Ox , co nie jest możliwe, bo parabola nie ma pionowych stycznych. W takim razie musi zachodzić drugi przypadek i kąt nachylenia stycznej do osi 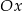Ox jest równy

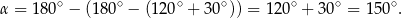
α = 180∘ − (180∘ − (120 ∘ + 3 0∘)) = 120∘ + 30∘ = 150∘.

Współczynnik kierunkowy stycznej jest więc równy

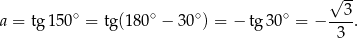
√ -- ∘ ∘ ∘ ∘ --3- a = tg 150 = tg (180 − 30 ) = − tg 30 = − 3 .

Liczymy teraz pochodną danej funkcji

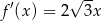
√ -- f′(x) = 2 3x

i sprawdzamy w jakim punkcie jest ona równa 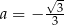√- a = − -3- 3 .

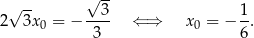
√ -- √ -- 3 1 2 3x0 = − ---- ⇐ ⇒ x0 = − -. 3 6

Stąd

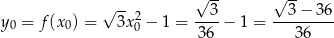
√ -- √ -- √ --2 --3- --3-−-3-6 y0 = f (x0) = 3x0 − 1 = 36 − 1 = 3 6

i 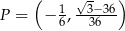( √- ) P = − 16, -33−636- .

PIC

 
Odpowiedź: ( √- ) ( √- ) P = − 16, 336-− 1 = − 16, -33−636-

Wersja PDF