/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu/Wielomiany

Zadanie nr 8532619

Oblicz pole trójkąta ograniczonego osią 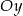Oy oraz stycznymi do wykresu funkcji 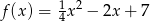f(x) = 14x2 − 2x + 7 poprowadzonymi w punktach 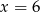x = 6 i x = 8 .

Wersja PDF

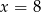Rozwiązanie

Korzystamy z równania stycznej do wykresu funkcji 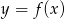y = f(x ) w punkcie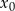 x 0

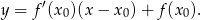
y = f′(x0)(x− x0)+ f(x0).

Liczymy

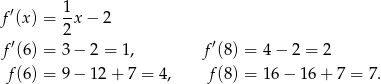
f′(x) = 1x − 2 2 f′(6) = 3 − 2 = 1, f′(8) = 4− 2 = 2 f(6) = 9 − 12 + 7 = 4, f (8) = 16 − 16 + 7 = 7.

Interesujące nas styczne mają więc równania

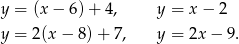
y = (x − 6) + 4, y = x − 2 y = 2(x − 8) + 7, y = 2x − 9.

Możemy teraz naszkicować całą sytuację.

PIC

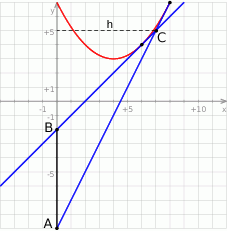
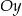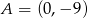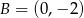Powyższe styczne przecinają oś Oy w punktach A = (0,− 9) i B = (0,− 2) . Podstawa 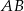AB trójkąta 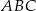ABC ma więc długość

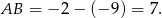
AB = − 2 − (− 9) = 7 .

Wyznaczamy teraz punkt wspólny 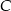C stycznych.

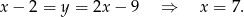
x − 2 = y = 2x − 9 ⇒ x = 7.

Zatem 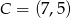C = (7,5) i wysokość trójkąta 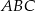ABC jest równa

h = 7.

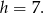
Pole trójkąta 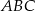ABC jest więc równe

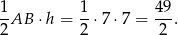
1- 1- 49- 2AB ⋅h = 2 ⋅7⋅ 7 = 2 .

 
Odpowiedź: 49 2

Wersja PDF