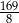Zadanie nr 8556683
Oblicz pole trójkąta ograniczonego osiami układu współrzędnych i styczną do paraboli 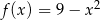 w punkcie
w punkcie 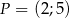 .
.
Rozwiązanie
Naszkicujmy sobie opisaną sytuację.
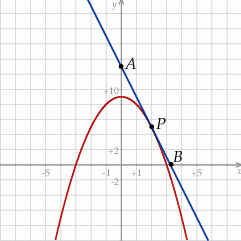
Widać, że musimy wyznaczyć współrzędne punktów 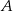 i
i 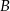 . Zrobimy to pisząc równanie stycznej do podanej paraboli, przechodzącej przez punkt
. Zrobimy to pisząc równanie stycznej do podanej paraboli, przechodzącej przez punkt 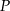 . Aby wyznaczyć współczynnik kierunkowy tej stycznej, liczymy pochodną funkcji
. Aby wyznaczyć współczynnik kierunkowy tej stycznej, liczymy pochodną funkcji 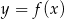 .
.
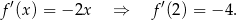
Zatem szukana styczna ma postać  . Ponieważ ma ona przechodzić przez
. Ponieważ ma ona przechodzić przez 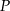 , mamy
, mamy
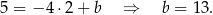
Otrzymujemy stąd 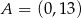 ,
, 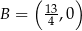 . Zatem szukane pole trójkąta prostokątnego
. Zatem szukane pole trójkąta prostokątnego  jest równe
jest równe
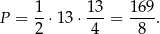
Odpowiedź: